Question

已知向量

a

，

b

，

c

满足|

a

|=|

b

|=3，

a

•

b

=

9

2

，若

a

-

c

与

c

-

b

的夹角为60°，则|

c

|的最大值为

2

3

．

Answer 1

分析：因为向量

a

，

b

满足|

a

|=|

b

|=3，

a

•

b

=

9

2

，所以可得两向量的夹角为60°，在平面内作出向量

OA

，

OB

，
使|

OA

|=|

OB

|=3，且两向量的夹角为60°，作出向量

OC

=

c

，由向量减法的几何意义得向量

a

-

c

与

c

-

b

，
再由

a

-

c

与

c

-

b

的夹角为60°，可得对应的O、A、C、B四点共圆，从而可知|

c

|的最大值为O、A、C、B四点共圆的圆的直径2R．然后运用正弦定理可求三角形ABC的外接圆的半径2R的值．

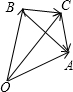解答：解：如图，
设

OA

=

a

，

OB

=

b

，

OC

=

c

，
由

a

•

b

=|

a

||

b

|cos＜

a

，

b

＞，
得：3×3×cos＜

a

，

b

＞=

9

2

，所以cos＜

a

，

b

＞=

1

2

，
所以∠AOB=60°．
又

a

-

c

=

OA

-

OC

=

CA

，

c

-

b

=

OC

-

OB

=

BC

，
由

a

-

c

与

c

-

b

的夹角为60°，得

CA

与

BC

的夹角为60°，则∠BCA=120°，
因为∠AOB+∠BCA=60°+120°=180°，
所以O、A、C、B四点共圆．
所以|

c

|的最大值为O、A、C、B四点共圆的圆的直径2R．
在三角形OAB中，因为|

OA

|=|

OB

|=3，∠AOB=60°，所以|AB|=3，
所以2R=

|AB|

sin60°

=

3

3 2

=2

3

．
所以，|

c

|的最大值为2

3

．
故答案为2

3

．

点评：本题考查了平面向量数量积的运算，考查了数形结合的解题思想，解答此题的关键是能够根据给出的向量夹角间的关系，分析得到三个向量

a

，

b

，

c

对应的向量

OA

，

OB

，

OC

的起点和终点四点共圆，从而得到|

c

|的最大值为O、A、C、B四点共圆的圆的直径2R．此题是中档题．