题目内容
(文)已知函数f(x)=x3-3ax+b(a≠0)在点(2,f(2))处与直线y=8相切,则双曲线 的离心率等于________.
的离心率等于________.
解:f′(x)=3x2-3a.依题意则有:f′(2)=3×22-3a=0,
且f(2)=23-3a×2+b=8
∴a=4,b=24,
则双曲线 的a=4,b=24,
的a=4,b=24,
∴c=
则双曲线 的离心率等于
的离心率等于

故答案为: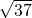 .
.
分析:先求出函数的导数,依题意则有:f′(2)=0,且f(2)=8,从而求出a=4,b=24,根据双曲线 的方程求得c=
的方程求得c= ,最后利用离心率公式即可求得双曲线
,最后利用离心率公式即可求得双曲线 的离心率.
的离心率.
点评:该题考查函数的求导、导数的几何意义,以及双曲线的简单性质.
且f(2)=23-3a×2+b=8
∴a=4,b=24,
则双曲线
 的a=4,b=24,
的a=4,b=24,∴c=

则双曲线
 的离心率等于
的离心率等于
故答案为:
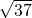 .
.分析:先求出函数的导数,依题意则有:f′(2)=0,且f(2)=8,从而求出a=4,b=24,根据双曲线
 的方程求得c=
的方程求得c= ,最后利用离心率公式即可求得双曲线
,最后利用离心率公式即可求得双曲线 的离心率.
的离心率.点评:该题考查函数的求导、导数的几何意义,以及双曲线的简单性质.

练习册系列答案
相关题目
 (文)已知函数f(x)=x3+ax2+bx+2与直线4x-y+5=0切于点P(-1,1).
(文)已知函数f(x)=x3+ax2+bx+2与直线4x-y+5=0切于点P(-1,1).