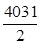题目内容
已知函数 在
在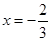 与
与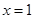 时都取得极值.
时都取得极值.
(1)求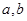 的值与函数
的值与函数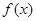 的单调区间
的单调区间
(2)若对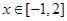 ,不等式
,不等式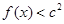 恒成立,求
恒成立,求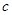 的取值范围.
的取值范围.
 在
在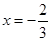 与
与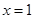 时都取得极值.
时都取得极值.(1)求
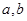 的值与函数
的值与函数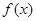 的单调区间
的单调区间(2)若对
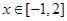 ,不等式
,不等式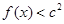 恒成立,求
恒成立,求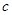 的取值范围.
的取值范围.(1) ,函数
,函数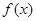 的递增区间是
的递增区间是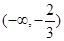 与
与 ,递减区间是
,递减区间是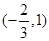 ;(2)
;(2)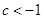 或
或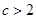 .
.
 ,函数
,函数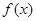 的递增区间是
的递增区间是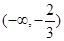 与
与 ,递减区间是
,递减区间是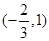 ;(2)
;(2)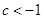 或
或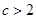 .
.试题分析:(1)先求出
 ,进而得到
,进而得到 ,从中解方程组即可得到
,从中解方程组即可得到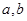 的值,然后再通过
的值,然后再通过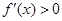 求出函数
求出函数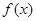 的增区间,通过
的增区间,通过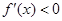 求出函数
求出函数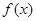 的减区间; (2)要使对
的减区间; (2)要使对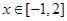 ,不等式
,不等式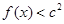 恒成立问题,则只需
恒成立问题,则只需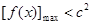 ,从而目标转向函数
,从而目标转向函数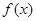 的最大值,根据(1)中所得的
的最大值,根据(1)中所得的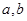 值,确定函数
值,确定函数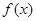 在区间
在区间 的最大值,进而求解不等式
的最大值,进而求解不等式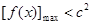 即可.
即可.试题解析:(1)

由
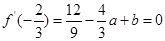 ,
, 得
得
 ,函数
,函数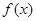 的单调区间如下表:
的单调区间如下表:  | 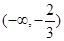 | 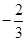 | 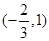 | |  |
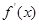 |  |  | 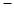 |  |  |
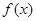 | | 极大值 | ¯ | 极小值 | |
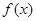 的递增区间是
的递增区间是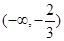 与
与 ,递减区间是
,递减区间是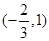
(2)
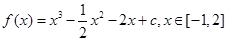 ,当
,当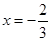 时,
时,
为极大值,而
 ,则
,则 为最大值,要使
为最大值,要使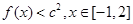
恒成立,则只需要
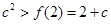 ,得
,得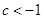 或
或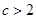 .
.
练习册系列答案
相关题目
 .
. ),f(
),f( )是否成等比数列,并证明f(
)是否成等比数列,并证明f( 为a、b的调和平均数,记为H.若H≤f(x)≤G,求x的取值范围.
为a、b的调和平均数,记为H.若H≤f(x)≤G,求x的取值范围.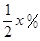 ,该产品每吨的价格上涨百分之几,可使销售的总金额最大?
,该产品每吨的价格上涨百分之几,可使销售的总金额最大? ,
, .
. ;
;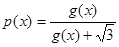 ,求证:
,求证: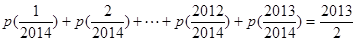 ;
; 是实数集
是实数集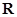 上的奇函数,且
上的奇函数,且 对任意实数
对任意实数 恒成立,求实数
恒成立,求实数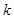 的取值范围.
的取值范围.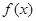 的定义域为R,若存在常数M>0,使
的定义域为R,若存在常数M>0,使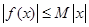 对一切实数x均成 立,则称
对一切实数x均成 立,则称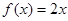 :②
:②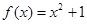 :③
:③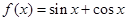 ;④
;④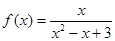 ⑤
⑤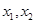 均有
均有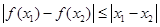 ,其中是“倍约束函数”的有( )
,其中是“倍约束函数”的有( ) 则函数
则函数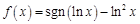 的零点个数为( ).
的零点个数为( ). B.
B.  C.
C.  D.
D. 
 ,若
,若 则
则 ( )
( )



 ,则
,则 ( )
( )