题目内容
(2013•临沂一模)设f(x)=ex(ax2+x+1).
(I)若a>0,讨论f(x)的单调性;
(Ⅱ)x=1时,f(x)有极值,证明:当θ∈[0,
]时,|f(cosθ)-f(sinθ)|<2.
(I)若a>0,讨论f(x)的单调性;
(Ⅱ)x=1时,f(x)有极值,证明:当θ∈[0,
| π | 2 |
分析:(I)利用导数的运算法则可得f′(x)=aex(x+
)(x+2),通过分类讨论
与2的大小关系,再根据导数与函数单调性的关系即可得出单调区间;
(II)由x=1时,f(x)有极值,得到f′(1)=0,即可得到a的值,再求出其单调递增区间,即可得出.
| 1 |
| a |
| 1 |
| a |
(II)由x=1时,f(x)有极值,得到f′(1)=0,即可得到a的值,再求出其单调递增区间,即可得出.
解答:解:(I)f′(x)=ex(ax2+x+1)+ex(2ax+1)=ex[ax2+(2a+1)x+2]=aex(x+
)(x+2).
(i)当a=
时,f′(x)=
ex(x+2)2≥0恒成立,∴函数f(x)在R上单调递增.
(ii)当0<a<
时,则
>2,即-
<-2.
由f′(x)>0,解得x>-2或x<-
;当f′(x)<0时,解得-
<x<-2.
∴函数f(x)在区间(-∞,-
)和(-2,+∞)上单调递增;在(-
,-2)上单调递减.
(iii)当a>
时,则
<2,即-
>-2.
由f′(x)>0,解得x>-
或x<-2;由f′(x)<0,解得-2<x<-
.
∴函数f(x)在区间(-∞,-2)和(-
,+∞)上单调递增;在(-2,-
)上单调递减.
(II)∵当x=1时,f(x)有极值,∴f′(1)=0.∴3ae(1+
)=0,解得a=-1.
∴f(x)=ex(-x2+x+1),f′(x)=-ex(x-1)(x+2).
令f′(x)>0,解得-2<x<1,∴f(x)在[-2,1]上单调递增,
∵sinθ,cosθ∈[0,1],∴|f(sinθ)-f(cosθ)|≤f(1)-f(0)=e-1<2.
| 1 |
| a |
(i)当a=
| 1 |
| 2 |
| 1 |
| 2 |
(ii)当0<a<
| 1 |
| 2 |
| 1 |
| a |
| 1 |
| a |
由f′(x)>0,解得x>-2或x<-
| 1 |
| a |
| 1 |
| a |
∴函数f(x)在区间(-∞,-
| 1 |
| a |
| 1 |
| a |
(iii)当a>
| 1 |
| 2 |
| 1 |
| a |
| 1 |
| a |
由f′(x)>0,解得x>-
| 1 |
| a |
| 1 |
| a |
∴函数f(x)在区间(-∞,-2)和(-
| 1 |
| a |
| 1 |
| a |
(II)∵当x=1时,f(x)有极值,∴f′(1)=0.∴3ae(1+
| 1 |
| a |
∴f(x)=ex(-x2+x+1),f′(x)=-ex(x-1)(x+2).
令f′(x)>0,解得-2<x<1,∴f(x)在[-2,1]上单调递增,
∵sinθ,cosθ∈[0,1],∴|f(sinθ)-f(cosθ)|≤f(1)-f(0)=e-1<2.
点评:本题综合考查了利用导数研究函数的单调性、极值、分类讨论思想方法等基础知识与方法,需要较强的推理能力和计算能力.

练习册系列答案
相关题目
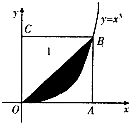 (2013•临沂一模)如图所示,在边长为l的正方形OABC中任取一点P,则点P恰好取自阴影部分的概率为( )
(2013•临沂一模)如图所示,在边长为l的正方形OABC中任取一点P,则点P恰好取自阴影部分的概率为( )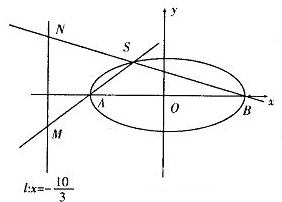 (2013•临沂一模)如图,已知椭圆C:
(2013•临沂一模)如图,已知椭圆C: