题目内容
15.已知过原点的直线l与曲线C:$\frac{{x}^{2}}{3}$+y2=1相交,直线l被曲线C所截得的线段长等于$\sqrt{6}$,则直线l的斜率k的-个取值是 ( )| A. | $\frac{\sqrt{3}}{3}$ | B. | $-\frac{\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | 1 |
分析 设直线l的方程为y=kx,与椭圆方程联立化为${x}^{2}=\frac{3}{1+3{k}^{2}}$,y2=$\frac{3{k}^{2}}{1+3{k}^{2}}$.利用$2\sqrt{{x}^{2}+{y}^{2}}$=$\sqrt{6}$,解出即可得出.
解答 解:设直线l的方程为y=kx,
联立$\left\{\begin{array}{l}{y=kx}\\{\frac{{x}^{2}}{3}+{y}^{2}=1}\end{array}\right.$,化为${x}^{2}=\frac{3}{1+3{k}^{2}}$,y2=$\frac{3{k}^{2}}{1+3{k}^{2}}$.
∴$2\sqrt{\frac{3}{1+3{k}^{2}}+\frac{3{k}^{2}}{1+3{k}^{2}}}$=$\sqrt{6}$,
化为:k2=1.
解得k=±1.
∴直线l的斜率k的-个取值是1.
故选:D.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交弦长问题,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.定义在R上的函数f(x)满足f(0)=0,f(x)+f(1-x)=1,f($\frac{x}{5}$)=$\frac{1}{2}f(x)$,且当0≤x1≤x2≤1时,f(x1)≤f(x2),则f($\frac{1}{2015}$)等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{16}$ | C. | $\frac{1}{32}$ | D. | $\frac{1}{64}$ |
20.满足“对定义域内的任意实数m,n,都有f(m•n)=f(m)+f(n)”的函数是( )
| A. | f(x)=x3 | B. | f(x)=kx(k≠0) | C. | f(x)=a-x | D. | f(x)=loga|x| |
20.执行如图所示的程序框图,则输出s的值为( )
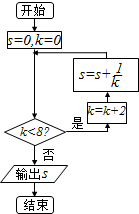

| A. | $\frac{25}{24}$ | B. | $\frac{11}{12}$ | C. | $\frac{5}{6}$ | D. | $\frac{3}{4}$ |