题目内容
(本小题满分12分)已知命题 :在
:在 上定义运算
上定义运算 :
: 不等式
不等式 对任意实数
对任意实数 恒成立;命题
恒成立;命题 :若不等式
:若不等式 对任意的
对任意的 恒成立.若
恒成立.若 为假命题,
为假命题, 为真命题,求实数
为真命题,求实数 的取值范围.
的取值范围.

【解析】
试题分析:解决该类问题的关键是要明确命题为真命题时对应的参数的取值范围,根据题的结论,判断命题的真假情况,从而判断出真命题的个数,最后确定参数的取值范围.
试题解析:由题意知,
若命题 为真,
为真, 对任意实数
对任意实数 恒成立, 1分
恒成立, 1分
 ①当
①当 即
即 时,
时, 恒成立,
恒成立, ; 2分
; 2分
②当 时,
时, ,
, , 3分
, 3分
综合①②得, 4分
4分
若命题 为真,
为真, ,
, ,
,
则有 对任意的
对任意的 恒成立 , 5分
恒成立 , 5分
即 对任意的
对任意的 恒成立,
恒成立,
令 ,只需
,只需 , 6分
, 6分
 ,当且仅当
,当且仅当 即
即 时取“=”
时取“=”
 8分
8分

 为假命题,
为假命题, 为真命题,
为真命题, 中必有一个真命题,一个假命题, 9分
中必有一个真命题,一个假命题, 9分
(1)若 为真
为真 为假,则
为假,则 ,
, , 10分
, 10分
(2)若 为假
为假 为真,则
为真,则 ,
, , 11分
, 11分
综上: 12分
12分
考点:复合命题的真值表,恒成立问题.
考点分析: 考点1:命题及其关系 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,集合
,集合 ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
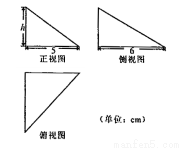
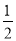

 的焦距为
的焦距为 ,点
,点 在
在 的渐近线上,则
的渐近线上,则 的方程为( )
的方程为( )
 B.
B.


 D.
D.
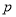 :
: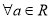 ,函数
,函数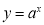 是单调函数,则
是单调函数,则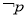 :( )
:( )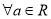 ,函数
,函数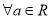 ,函数
,函数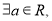 函数
函数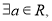 函数
函数 的棱长为
的棱长为 ,设
,设 ,则
,则 .
.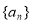 是首项为
是首项为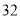 的等比数列,
的等比数列, 是其前
是其前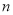 项和,且
项和,且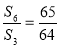 ,则数列
,则数列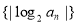 前
前 项和为( )
项和为( ) B.
B.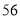 C.
C. D.
D.
 满足:
满足: 成等差数列,且对任意的正整数n,均有
成等差数列,且对任意的正整数n,均有 成立,其中
成立,其中 是数列
是数列 ; (2)求数列
; (2)求数列 上的圆C与
上的圆C与 轴交于两点
轴交于两点 ,
, ,则圆C的方程为 .
,则圆C的方程为 .