题目内容
已知函数f(x)=ex,函数g(x)的图象与f(x)的图象关于直线y=x对称,h(x)=kx+b.(Ⅰ)当b=0时,若对?x∈(0,+∞)均有f(x)≥h(x)≥g(x)成立,求实数k的取值范围;
(Ⅱ)设h(x)的图象与f(x)的图象和g(x)的图象均相切,切点分别为
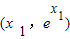 和(x2,g(x2)),其中x1>0.
和(x2,g(x2)),其中x1>0.(1)求证:x1>1>x2;
(2)若当x≥x1时,关于x的不等式
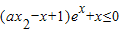 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
【答案】分析:(Ⅰ)根据f(x)与g(x)图象的对称关系求出g(x),当b=0时数形结合,令h(x)与f(x)、g(x)分别相切,此时求出k值即为最大、最小值.
(Ⅱ)(1)由所给条件知,此时h(x)为f(x)、g(x)的公切线,则两切点处导数相等,且与其连线斜率也相等,再结合x1>0即可证明.
(2)先把x1、x2当作常数,分离参数后转化函数最值问题,再把x1、x2当作变量用导数求函数最值即可解决.
解答:(Ⅰ)解:因为函数g(x)的图象与f(x)的图象关于直线y=x对称,所以g(x)=lnx.
当b=0时,h(x)=kx,当f(x)与y=kx相切时,设切点为(x1,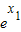 ),则有
),则有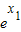 =
=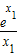 =k,∴x1=1,k=e.
=k,∴x1=1,k=e.
当g(x)与y=kx相切时,设切点为(x2,lnx2),则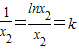 ,∴x2=e,k=
,∴x2=e,k=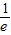 .
.
因为对?x∈(0,+∞)均有f(x)≥h(x)≥g(x)成立,据图象有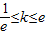 ,
,
故实数k的取值范围为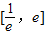 .
.
(Ⅱ)(1)由题意得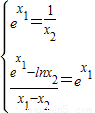 ,
,
∵x1>0,∴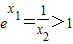 ,∴0<x2<1.
,∴0<x2<1.
由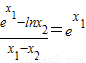 得
得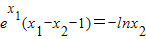 ,
,
∵0<x2<1,∴-lnx2>0,∴x1-x2-1>0,x1>x2+1>1.
综上,x1>1>x2.
(2)∵x1>1>x2>0,∴关于x的不等式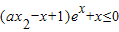 恒成立,即ax2≤-xe-x+x-1恒成立,
恒成立,即ax2≤-xe-x+x-1恒成立,
令m(x)=-xe-x+x-1,则m′(x)=(x-1)e-x+1,当x≥x1>1时,m′(x)>0,所以m(x)单调递增,m(x)≥m(x1)=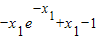 .
.
所以ax2≤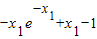 ,a≤
,a≤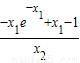 ,又
,又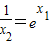 ,所以a≤-x1+(x1-1)
,所以a≤-x1+(x1-1)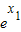 ,
,
令n(x1)=-x1+(x1-1)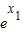 ,则n′(x1)=-1+
,则n′(x1)=-1+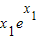 ,因为x1>1,所以n′(x1)>0,n(x1)单调递增,n(x1)>n(1)=-1,所以a≤-1.
,因为x1>1,所以n′(x1)>0,n(x1)单调递增,n(x1)>n(1)=-1,所以a≤-1.
故实数a的取值范围为:a≤-1.
点评:本题属函数恒成立问题,综合性强,难度大,对分析问题解决问题的能力要求较高.
(Ⅱ)(1)由所给条件知,此时h(x)为f(x)、g(x)的公切线,则两切点处导数相等,且与其连线斜率也相等,再结合x1>0即可证明.
(2)先把x1、x2当作常数,分离参数后转化函数最值问题,再把x1、x2当作变量用导数求函数最值即可解决.
解答:(Ⅰ)解:因为函数g(x)的图象与f(x)的图象关于直线y=x对称,所以g(x)=lnx.
当b=0时,h(x)=kx,当f(x)与y=kx相切时,设切点为(x1,
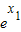 ),则有
),则有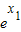 =
=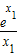 =k,∴x1=1,k=e.
=k,∴x1=1,k=e.当g(x)与y=kx相切时,设切点为(x2,lnx2),则
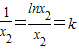 ,∴x2=e,k=
,∴x2=e,k=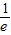 .
.因为对?x∈(0,+∞)均有f(x)≥h(x)≥g(x)成立,据图象有
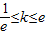 ,
,故实数k的取值范围为
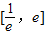 .
.(Ⅱ)(1)由题意得
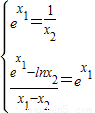 ,
,∵x1>0,∴
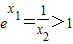 ,∴0<x2<1.
,∴0<x2<1.由
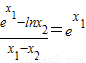 得
得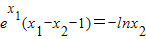 ,
,∵0<x2<1,∴-lnx2>0,∴x1-x2-1>0,x1>x2+1>1.
综上,x1>1>x2.
(2)∵x1>1>x2>0,∴关于x的不等式
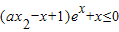 恒成立,即ax2≤-xe-x+x-1恒成立,
恒成立,即ax2≤-xe-x+x-1恒成立,令m(x)=-xe-x+x-1,则m′(x)=(x-1)e-x+1,当x≥x1>1时,m′(x)>0,所以m(x)单调递增,m(x)≥m(x1)=
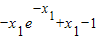 .
.所以ax2≤
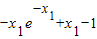 ,a≤
,a≤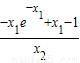 ,又
,又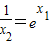 ,所以a≤-x1+(x1-1)
,所以a≤-x1+(x1-1)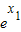 ,
,令n(x1)=-x1+(x1-1)
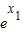 ,则n′(x1)=-1+
,则n′(x1)=-1+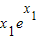 ,因为x1>1,所以n′(x1)>0,n(x1)单调递增,n(x1)>n(1)=-1,所以a≤-1.
,因为x1>1,所以n′(x1)>0,n(x1)单调递增,n(x1)>n(1)=-1,所以a≤-1.故实数a的取值范围为:a≤-1.
点评:本题属函数恒成立问题,综合性强,难度大,对分析问题解决问题的能力要求较高.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目