Question

解不等式|x²－3x－4|＞x+1.?

Answer 1

解法一：当x＜－1时，不等式显然成立；?

当x=－1时，不等式不成立；?

当x＞－1时，原不等式化为?

（1）或（2）

解（1）得x＞5，

解（2）得－1＜x＜3.?

故原不等式的解集为(－∞,－1)∪(－1,3)∪(5,+∞).?

解法二：原不等式等价于?

（1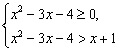）或（2）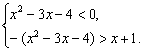

解（1）得x＜－1或x＞5,解（2）得－1＜x＜3.?

故原不等式的解集为（－∞,－1）∪（－1，3）∪（5，+∞）.

解法三：考察函数y=|x²－3x－4|和函数y=x+1的图象：如下图所示，由图象可知原不等式的解为(－∞,－1)∪(－1,3)∪(5,+∞).?

点评：解法一与解法二是将原不等式转化成等价的不等式进行求解,解法三是利用数形结合来求解.应当注意的是：在解法一和解法二中，求原不等式的解集应是两不等式组的交集；在解法三中，应确保交点坐标准确无误.