题目内容
已知f(x)是定义在R上的奇函数,当x≥0时,f(x)=ax-1.其中a>0且a≠1.(1)求f(2012)+f(-2012)的值;
(2)求f(x)的解析式;
(3)当a=2时,解关于x的不等式-1<f(x-1)<4,结果用集合或区间表示.
【答案】分析:(1)利用奇函数的定义可以得出f(-x)+f(x)=0,从而求得所求的式子的值.
(2)根据奇函数的定义可得f(0)=0.设xx≤0,则-x≥0,再根据条件求得此时f(x)的解析式,从而得出结论.
(3)故当x≥0时,有-1<2x-1-1<4,由此求得x的范围.当x<0时,-1<1-2-(x-1)<4,由此求得x的范围.最后再把这2个x的范围取并集,即得所求.
解答:解:(1)由奇函数的定义可得f(2012)+f(-2012)=f(2012)-f(2012)=0.
(2)设x≤0,则-x≥0,故有f(-x)=a-x-1=-f(x),∴f(x)=1-a-x.
由此可得 f(x)=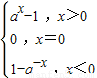 .
.
(3)由于a=2,故当x≥0时,有-1<2x-1-1<4,即0<2x-1<5,所以x∈(0,log210).
当x<0时,-1<1-2-(x-1)<4,所以,不等式无解
综上所述,不等式的解集为 (0,log210).
点评:本题考查了奇函数的性质、求函数的解析式、以及对数函数不等式的解法,属于中档题.
(2)根据奇函数的定义可得f(0)=0.设xx≤0,则-x≥0,再根据条件求得此时f(x)的解析式,从而得出结论.
(3)故当x≥0时,有-1<2x-1-1<4,由此求得x的范围.当x<0时,-1<1-2-(x-1)<4,由此求得x的范围.最后再把这2个x的范围取并集,即得所求.
解答:解:(1)由奇函数的定义可得f(2012)+f(-2012)=f(2012)-f(2012)=0.
(2)设x≤0,则-x≥0,故有f(-x)=a-x-1=-f(x),∴f(x)=1-a-x.
由此可得 f(x)=
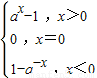 .
.(3)由于a=2,故当x≥0时,有-1<2x-1-1<4,即0<2x-1<5,所以x∈(0,log210).
当x<0时,-1<1-2-(x-1)<4,所以,不等式无解
综上所述,不等式的解集为 (0,log210).
点评:本题考查了奇函数的性质、求函数的解析式、以及对数函数不等式的解法,属于中档题.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目