题目内容
 (2013•天河区三模)如图,在矩形ABCD中,AB=2BC=12,E为CD的中点,将△DAE沿AE折起,使面DAE⊥面ABCE;再过点D作DQ∥AB,且DQ=
(2013•天河区三模)如图,在矩形ABCD中,AB=2BC=12,E为CD的中点,将△DAE沿AE折起,使面DAE⊥面ABCE;再过点D作DQ∥AB,且DQ=| 1 | 2 |
(Ⅰ)求证:面DAE⊥面BEQ;
(Ⅱ)求直线BD与面DAE所成角的正弦值;
(Ⅲ)求点Q到面DAE的距离.
分析:(I)利用勾股定理的逆定理可知BE⊥AE,再利用面面垂直的性质定理可得BE⊥平面DAE,利用面面垂直的判定定理即可证明结论;
(II)由(I)知,BE⊥平面DAE,可得∠BDE是直线BD与平面DAE所成的角,再利用直角三角形的边角关系即可求出;
(III)设点Q到平面DAE的距离为h,由DQ∥EC且DQ=EC,可得四边形DQCE为平行四边形,得到QC∥DE,从而QC∥平面DAE,故点Q到平面DAE的距离等于点C到平面DAE 的距离.作DH⊥AE与H,由面DAE⊥面BEQ,交线为AE,可得AH⊥平面ABCE,则AH是D到面ABCE的距离,再利用“等体积变形”VQ-ADE=VC-ADE=VD-AEC,即可得出.
(II)由(I)知,BE⊥平面DAE,可得∠BDE是直线BD与平面DAE所成的角,再利用直角三角形的边角关系即可求出;
(III)设点Q到平面DAE的距离为h,由DQ∥EC且DQ=EC,可得四边形DQCE为平行四边形,得到QC∥DE,从而QC∥平面DAE,故点Q到平面DAE的距离等于点C到平面DAE 的距离.作DH⊥AE与H,由面DAE⊥面BEQ,交线为AE,可得AH⊥平面ABCE,则AH是D到面ABCE的距离,再利用“等体积变形”VQ-ADE=VC-ADE=VD-AEC,即可得出.
解答: (I)证明:折叠前,矩形ABCD中,连接BE,
(I)证明:折叠前,矩形ABCD中,连接BE,
在△ABE中,AE=BE=6
,AB=12,
∴AE2+BE2=AB2,
∴AE⊥BE,
∵面DAE⊥面ABCE,交线为AE,
∴BE⊥平面DAE,
而BE?BEQ,∴面DAE⊥面BEQ;
(II)由(I)知,BE⊥平面DAE,∴∠BDE是直线BD与平面DAE所成的角,
在Rt△BDE中,BE=6
,DE=6,BD=6
∴sin∠BDE=
=
=
.
故直线BD与平面DAE所成角的正弦值为
.
(III)设点Q到平面DAE的距离为h,
∵DQ∥EC且DQ=EC,
∴四边形DQCE为平行四边形,
QC∥DE,从而QC∥平面DAE,
故点Q到平面DAE的距离等于点C到平面DAE 的距离,
作DH⊥AE与H,
∵面DAE⊥面BEQ,交线为AE,
∴DH⊥平面ABCE,则DH是D到面ABCE的距离,而DH=3
.
由VQ-ADE=VC-ADE=VD-AEC
∴
•S△ADE•h=
•S△AEC•DH,
又S△ADE=
•AD•DE=18,S△AEC=
•EC•AD=18.
∴h=3
.
∴点Q到平面DAE 的距离为3
.
 (I)证明:折叠前,矩形ABCD中,连接BE,
(I)证明:折叠前,矩形ABCD中,连接BE,在△ABE中,AE=BE=6
| 2 |
∴AE2+BE2=AB2,
∴AE⊥BE,
∵面DAE⊥面ABCE,交线为AE,
∴BE⊥平面DAE,
而BE?BEQ,∴面DAE⊥面BEQ;
(II)由(I)知,BE⊥平面DAE,∴∠BDE是直线BD与平面DAE所成的角,
在Rt△BDE中,BE=6
| 2 |
| 3 |
∴sin∠BDE=
| BE |
| BD |
6
| ||
6
|
| ||
| 3 |
故直线BD与平面DAE所成角的正弦值为
| ||
| 3 |
(III)设点Q到平面DAE的距离为h,
∵DQ∥EC且DQ=EC,
∴四边形DQCE为平行四边形,
QC∥DE,从而QC∥平面DAE,
故点Q到平面DAE的距离等于点C到平面DAE 的距离,
作DH⊥AE与H,
∵面DAE⊥面BEQ,交线为AE,
∴DH⊥平面ABCE,则DH是D到面ABCE的距离,而DH=3
| 2 |
由VQ-ADE=VC-ADE=VD-AEC
∴
| 1 |
| 3 |
| 1 |
| 3 |
又S△ADE=
| 1 |
| 2 |
| 1 |
| 2 |
∴h=3
| 2 |
∴点Q到平面DAE 的距离为3
| 2 |
点评:本题综合考查了线面垂直、面面垂直、线面角、三棱锥的体积等基础知识,需要较强的推理能力、计算能力和空间想象能力.

练习册系列答案
相关题目
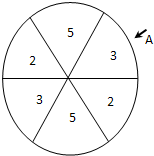 (2013•天河区三模)如图,一个圆形游戏转盘被分成6个均匀的扇形区域.用力旋转转盘,转盘停止转动时,箭头A所指区域的数字就是每次游戏所得的分数(箭头指向两个区域的边界时重新转动),且箭头A指向每个区域的可能性都是相等的.在一次家庭抽奖的活动中,要求每个家庭派一位儿童和一位成人先后分别转动一次游戏转盘,得分情况记为(a,b)(假设儿童和成人的得分互不影响,且每个家庭只能参加一次活动).
(2013•天河区三模)如图,一个圆形游戏转盘被分成6个均匀的扇形区域.用力旋转转盘,转盘停止转动时,箭头A所指区域的数字就是每次游戏所得的分数(箭头指向两个区域的边界时重新转动),且箭头A指向每个区域的可能性都是相等的.在一次家庭抽奖的活动中,要求每个家庭派一位儿童和一位成人先后分别转动一次游戏转盘,得分情况记为(a,b)(假设儿童和成人的得分互不影响,且每个家庭只能参加一次活动).