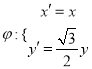题目内容
【题目】如果二面角α﹣L﹣β的大小是60°,线段AB在α内,AB与L所成的角为60°,则AB与平面β所成角的正切值是 .
【答案】![]()
【解析】解:过点A作平面β的垂线,垂足为C,在β内过C作l的垂线,垂足为D. 连结AD,根据三垂线定理可得AD⊥L,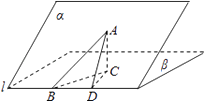
因此,∠ADC为二面角α﹣L﹣β的平面角,∠ADC=60°
又∵AB与L所成角为60°,
∴∠ABD=60°,
连结BC,可得BC为AB在平面β内的射影,
∴∠ABC为AB与平面β所成的角.
设AD=2x,则Rt△ACD中,AC=ADsin60°= ![]() x,
x,
Rt△ABD中,AB= ![]() =
= ![]() x
x
∴Rt△ABC中,sin∠ABC= ![]() =34,
=34,
∴tan∠ABC= ![]()
所以答案是: ![]() .
.
【考点精析】掌握空间角的异面直线所成的角是解答本题的根本,需要知道已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则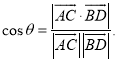 .
.

练习册系列答案
相关题目