题目内容
一直线l经过抛物线y2=4x的焦点,且与抛物线相交于A、B,若|AB|=8,求直线l的倾斜角.
解：由抛物线方程为y2=4x,得p=2,
焦点F(1,0),又|AB|=x1+x2+p=8,
∴x1+x2=6.
设l的斜率为k,则l:y=k(x-1).
由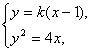
得k2x2-(2k2+4)x+k2=0.
∴x1+x2=
=2+
=6,k2=1,k=±1.
∴l的倾斜角为45°或135°.
练习册系列答案
相关题目
题目内容
一直线l经过抛物线y2=4x的焦点,且与抛物线相交于A、B,若|AB|=8,求直线l的倾斜角.
解：由抛物线方程为y2=4x,得p=2,
焦点F(1,0),又|AB|=x1+x2+p=8,
∴x1+x2=6.
设l的斜率为k,则l:y=k(x-1).
由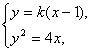得k2x2-(2k2+4)x+k2=0.
∴x1+x2==2+=6,k2=1,k=±1.
∴l的倾斜角为45°或135°.
如图，抛物线M：y=x2+bx（b≠0）与x轴交于O，A两点，交直线l：y=x于O，B两点，经过三点O，A，B作圆C．
，且与直线l：
相切，其中p＞0．