Question

在等差数列{a_n}中，共有3m项，前2m项的和为100，后2m项的和为200，求中间m项的和.

Answer 1

解法一:由已知

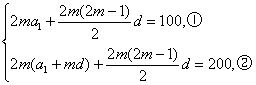
②－①整理得d=,代入①可得a₁=.

∴S_2m－S_m=m(a₁+md)+=m(+)+=75.

解法二:由已知S_m,S_2m－S_m,S_3m－S_2m成等差数列,即2(S_2m－S_m)=S_m+(S_3m－S_2m),

又由已知S_2m=100,S_3m－S_m=200,

∴S_2m－S_m===75.

点评:解法一利用了等差数列的前n项和公式,方法比较常规；解法二利用等差数列的性质,运算更为简洁、方便.