题目内容
已知函数f(x)=sin(2x+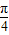 ),则下列命题正确的是( )
),则下列命题正确的是( )A.函数y=f(x)的图象关于点(
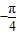 ,0)对称
,0)对称B.函数y=f(x)在区间(
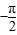 ,0)上是增函数
,0)上是增函数C.函数y=f(x+
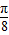 )是偶函数
)是偶函数D.将函数y=sin2x的图象向左平移
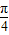 个单位得到函数y=f(x)的图象
个单位得到函数y=f(x)的图象
【答案】分析:求出函数f(x)的对应的对称中心和对称轴,即可判断A和C的正误;根据正弦函数的单调行可判断B不对;对根据左加右减的原则函数y=sin2x进行平移,进而可判断D;从而可判断答案.
解答:解:当2x+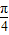 =kπ时,即x=
=kπ时,即x= kπ-
kπ-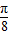 (k∈Z),函数y=f(x)的图象关于点(
(k∈Z),函数y=f(x)的图象关于点( kπ-
kπ-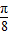 ,0)对称,当k=0时,点(
,0)对称,当k=0时,点( kπ-
kπ-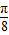 ,0)即点(-
,0)即点(-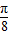 ,0).故选项A错;
,0).故选项A错;
由-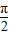 +2kπ≤2x+
+2kπ≤2x+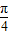 ≤
≤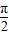 +2kπ,得-
+2kπ,得-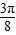 +kπ≤x≤
+kπ≤x≤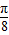 +kπ,
+kπ,
∴函数f(x)在区间(-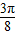 +kπ,
+kπ,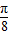 +kπ )上单调递增,当k=0时函数f(x)在区间(-
+kπ )上单调递增,当k=0时函数f(x)在区间(-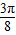 ,
,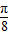 )上单调递增,故B不对;
)上单调递增,故B不对;
令2x+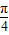 =
=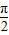 +kπ,∴x=
+kπ,∴x=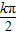 +
+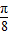 (k∈Z),故函数f(x)的对称轴是x=
(k∈Z),故函数f(x)的对称轴是x=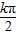 +
+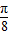 (k∈Z),故函数y=f(x+
(k∈Z),故函数y=f(x+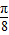 )对称轴是x=
)对称轴是x=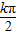 (k∈Z),
(k∈Z),
当k=0时,即关于y轴对称,故是偶函数,故C对;
将函数y=sin2x的图象向左平移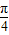 个单位得到函数y=sin(2x+
个单位得到函数y=sin(2x+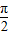 )的图象,不是函数f(x),D不对.
)的图象,不是函数f(x),D不对.
故选C.
点评:本题主要考查三角函数的基本性质--单调性与对称性.高考对三角函数的考查以基础题为主,平时要注意基础知识的积累,到高考时才能做到游刃有余.
解答:解:当2x+
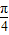 =kπ时,即x=
=kπ时,即x= kπ-
kπ-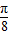 (k∈Z),函数y=f(x)的图象关于点(
(k∈Z),函数y=f(x)的图象关于点( kπ-
kπ-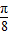 ,0)对称,当k=0时,点(
,0)对称,当k=0时,点( kπ-
kπ-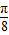 ,0)即点(-
,0)即点(-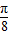 ,0).故选项A错;
,0).故选项A错;由-
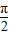 +2kπ≤2x+
+2kπ≤2x+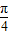 ≤
≤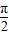 +2kπ,得-
+2kπ,得-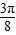 +kπ≤x≤
+kπ≤x≤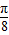 +kπ,
+kπ,∴函数f(x)在区间(-
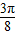 +kπ,
+kπ,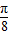 +kπ )上单调递增,当k=0时函数f(x)在区间(-
+kπ )上单调递增,当k=0时函数f(x)在区间(-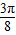 ,
,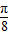 )上单调递增,故B不对;
)上单调递增,故B不对;令2x+
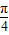 =
=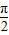 +kπ,∴x=
+kπ,∴x=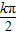 +
+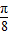 (k∈Z),故函数f(x)的对称轴是x=
(k∈Z),故函数f(x)的对称轴是x=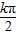 +
+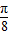 (k∈Z),故函数y=f(x+
(k∈Z),故函数y=f(x+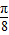 )对称轴是x=
)对称轴是x=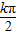 (k∈Z),
(k∈Z),当k=0时,即关于y轴对称,故是偶函数,故C对;
将函数y=sin2x的图象向左平移
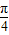 个单位得到函数y=sin(2x+
个单位得到函数y=sin(2x+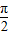 )的图象,不是函数f(x),D不对.
)的图象,不是函数f(x),D不对.故选C.
点评:本题主要考查三角函数的基本性质--单调性与对称性.高考对三角函数的考查以基础题为主,平时要注意基础知识的积累,到高考时才能做到游刃有余.

练习册系列答案
相关题目
