题目内容
若 且点
且点 在过点
在过点 的直线上,则
的直线上,则 的最大值是
的最大值是
A. | B. | C. | D. |
D
解析考点:基本不等式;直线的两点式方程.
分析:由点(a,b)在过点(1,-1)和(2,-3)的直线上得2a+b=1,所以S="2"  -4a2-b2="4ab+2"
-4a2-b2="4ab+2"  -1,再令
-1,再令  =t>0,则S化为关于t的二次函数形式,再由二次函数的性质结合t的取值范围可得S的最大值.
=t>0,则S化为关于t的二次函数形式,再由二次函数的性质结合t的取值范围可得S的最大值.
解:过点(1,-1),(2,-3)的直线方程为: =
= ,2x+y-1=0.
,2x+y-1=0.
∴2a+b-1=0,即2a+b=1.
S="2"  -4a2-b2="4ab+2"
-4a2-b2="4ab+2"  -(2a+b)2="4ab+2"
-(2a+b)2="4ab+2"  -1
-1
令  =t,∵a>0,b>0,∴2a+b=1≥2
=t,∵a>0,b>0,∴2a+b=1≥2 ,∴0<
,∴0< ≤
≤ ,即 0<t ≤
,即 0<t ≤ ,
,
则 S=4t2+2t-1,在(0,+∞)上为增函数
故 当t= 时,S 有最大值
时,S 有最大值  ,
,
故答案为:D.

练习册系列答案
相关题目
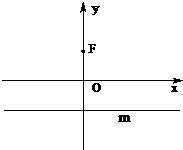 (2013•嘉定区二模)如图,已知点F(0,1),直线m:y=-1,P为平面上的动点,过点P作m的垂线,垂足为点Q,且
(2013•嘉定区二模)如图,已知点F(0,1),直线m:y=-1,P为平面上的动点,过点P作m的垂线,垂足为点Q,且 ,且点
,且点 在过点
在过点 、
、 的直线上,则
的直线上,则 的最大值是 .
的最大值是 .