Question

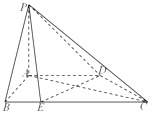
【题目】如图，在四棱锥PABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC＝60°，PA＝AB＝BC，E是PC的中点．

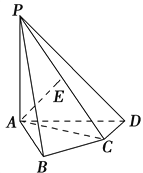
(1)证明：AE⊥平面PCD；

(2)求二面角A－PD－C的正弦值．

Answer 1

【答案】（1）见解析；（2）.

【解析】试题分析：（1）通过和得到 平面，利用等腰三角形的性质可得，可得结论；（2）过点作，垂足为，连接，证得是二面角的平面角，在中先求出，然后在中求出结论.

试题解析：(1)证明：在四棱锥中，因底面， 平面，

故.由条件， ，∴平面.

又平面，∴.

由， ，可得.

∵是的中点，∴.

又，综上得平面.

（2）过点作，垂足为，连接，

由（1）知， 平面， 在平面内的射影是，则．

因此是二面角的平面角．

由已知，可得．设，可得， ，

， ．

在中，∵，∴，则 ，

在中， .