题目内容
已知函数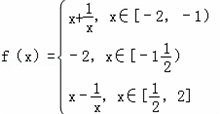
(1)求f(x)的值域
(2)设函数g(x)=ax﹣2,x∈[﹣2,2],对于任意x1∈[﹣2,2],总存在x0∈[﹣2,2],使得g(x0)=f(x1)成立,求实数a的取值范围.
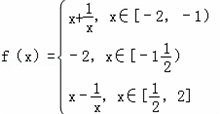
(1)求f(x)的值域
(2)设函数g(x)=ax﹣2,x∈[﹣2,2],对于任意x1∈[﹣2,2],总存在x0∈[﹣2,2],使得g(x0)=f(x1)成立,求实数a的取值范围.
解:(1)当x∈[-2,2]时,f(x)=x+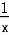 在[-2,-1]上是增函数,
在[-2,-1]上是增函数,
此时f(x)∈[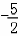 ,-2]
,-2]
当x∈[-1,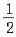 )时,f(x)=-2
)时,f(x)=-2
当x∈[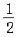 ,2]时,f(x)= x-
,2]时,f(x)= x-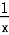 在[
在[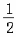 ,2]上是增函数,
,2]上是增函数,
此时f(x)∈[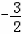 ,
,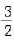 ]
]
∴f(x)的值域为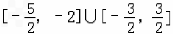
(2)①若a=0,g(x)=﹣2,对于任意x1∈[-2,2],
f(x1)∈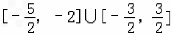 ,
,
不存在x0∈[-2,2],使g(x0)=f(x1)
②当a>0时,g(x)=ax﹣2在[﹣2,2]是增函数,g(x)∈[﹣2a﹣2,2a﹣2]
任给x1∈[-2,2],f(x1)∈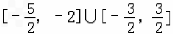
若存在x0∈[﹣2,2],使得g(x0)=f(x1)成立
则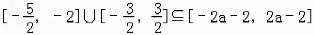
∴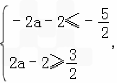
∴a≥
③a<0,g(x)=ax﹣2在[﹣2,2]是减函数,g(x)∈[2a﹣2,﹣2a﹣2]
∴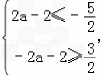
∴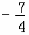
综上,实数a∈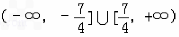

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


 上恒成立,求实数m的取值范围.
上恒成立,求实数m的取值范围.

