题目内容
函数y=3sin（-2x-
）（x∈[0，π]）的单调递增区间是
- A.[0，
] - B.[，
] - C.[，
] - D.[，]
B
分析：先利用三角函数的诱导公式将三角函数中x的系数化为正的，将函数y=3sin（-2x-）（x∈[0，π]）的单调递增区间转化为函数y=3sin（2x+）的递减区间，然后通过整体角处理的方法来解决．
解答：因为y=3sin（-2x-）=-3sin（2x+）
所以函数y=3sin（-2x-）（x∈[0，π]）的单调递增区间是函数y=3sin（2x+）的递减区间，
令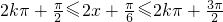
，
解得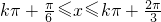
，
又因为x∈[0，π]，
所以x∈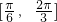
，
故选B．
点评：本题考查再解决三角函数的性质问题时，常采用的手段是整体角处理，注意应该先将x的系数化为正，属于基础题．
分析：先利用三角函数的诱导公式将三角函数中x的系数化为正的，将函数y=3sin（-2x-
）（x∈[0，π]）的单调递增区间转化为函数y=3sin（2x+）的递减区间，然后通过整体角处理的方法来解决．解答：因为y=3sin（-2x-
）=-3sin（2x+）所以函数y=3sin（-2x-
）（x∈[0，π]）的单调递增区间是函数y=3sin（2x+）的递减区间，令
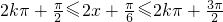，解得
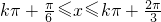，又因为x∈[0，π]，
所以x∈
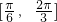，故选B．
点评：本题考查再解决三角函数的性质问题时，常采用的手段是整体角处理，注意应该先将x的系数化为正，属于基础题．
练习册系列答案
相关题目