题目内容
设直线l与抛物线y=-
解析:设直线l的方程为y=kx+b(b<0),联立抛物线方程消去y,得kx+b=-![]() ,即x2+2kx+2b=0.
,即x2+2kx+2b=0.
设A(x1,y1)、B(x2,y2),则x1+x2=-2k,x1x2=2b.
∵kOA+kOB=1,∴![]() =1,即
=1,即
x1x2=x1y2+x2y1.又y1=kx1+b,y2=kx2+b,
∴x1x2=x1(kx2+b)+x2(kx1+b),
即(2k-1)x1x2+b(x1+x2)=0.
于是有(2k-1)·2b+b·(-2k)=0.根据题意b≠0,
∴2(2k-1)-2k=0,解得k=1.
故直线l的斜率为1.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
 已知抛物线的顶点在坐标原点O,焦点F在x轴正半轴上,倾斜角为锐角的直线l过F点,设直线l与抛物线交于A、B两点,与抛物线的准线交于M点,
已知抛物线的顶点在坐标原点O,焦点F在x轴正半轴上,倾斜角为锐角的直线l过F点,设直线l与抛物线交于A、B两点,与抛物线的准线交于M点,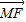 =λ
=λ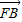 (λ>0)
(λ>0)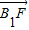 |,|
|,|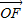 |,2|
|,2|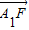 |成等差数列求λ的值
|成等差数列求λ的值