题目内容

已知数列{an}是等差数列，a2=6，a5=18，数列{bn}的前n项和是Tn,且Tn+bn=1．

(Ⅰ)求数列{an}的通项公式；

(Ⅱ)求证数列{bn}是等比数列；

(Ⅲ)记cn=an·bn，求证cn+1≤cn．

解：(Ⅰ)由已知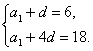  解得a1=2，d=4．

∴an=2+(n-1)×4=4n-2.

(Ⅱ)由于Tn=1-bn，     ①

令n=1，得b1=1-b1，解得b1=．

当n≥2时，Tn-l=1-bn-1.   ②

①-②得bn=bn-1-bn,

∴bn=bn-1. 又b1=≠0，

∴.

∴数列{bn}是以为首项，为公比的等比数列．

(Ⅲ)由(Ⅱ)可得bn=.

cn=an·bn=(4n-2)=．

cn+1-cn=．

∵n≥1，故cn+1-cn≤0．

∴cn+1≤cn．

练习册系列答案
相关题目
定义一个“等积数列”：在一个数列中，如果每一项与它后一项的积都是同一常数，那么这个数列叫“等积数列”，这个常数叫做这个数列的公积．已知数列{an}是等积数列，且a1=2，公积为5，则这个数列的前n项和Sn的计算公式为：
 
．
在一个数列中，如果?n∈N*，都有an•an+1•an+2=k（k为常数），那么这个数列叫做等积数列，k叫做这个数列的公积．已知数列{an}是等积数列，且a1=1，a2=3，公积为27，则a1+a2+a3+…+a18=
78
78
．
定义“等积数列”：在一个数列中，如果每一个项与它的后一项的积都为同一个常数，那末这个数列叫做等积数列，这个常数叫做该数列的公积．已知数列{an}是等积数列，且a1=2，公积为5，Tn为数列{an}前n项的积，则T2011=
51006
2
51006
2
．
我们对数列作如下定义，如果?n∈N*，都有anan+1an+2=k（k为常数），那么这个数列叫做等积数列，k叫做这个数列的公积．已知数列{an}是等积数列，且a1=1，a2=2，公积为6，则a1+a2+a3+…+a9=
18
18
．
已知等差数列的定义为：在一个数列中，从第二项起，如果每一项与它的前一项的差都为同一个常数，那么这个数列叫做等差数列，这个常数叫做该数列的公差．
（1）类比等差数列的定义给出“等和数列”的定义；
（2）已知数列{an}是等和数列，且a1=2，公和为5，求 a18的值，并猜出这个数列的通项公式（不要求证明）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网