题目内容
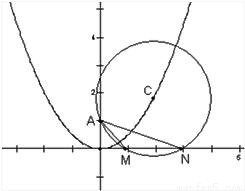
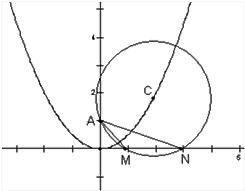 已知:圆C过定点A(0,p),圆心C在抛物线x2=2py上运动,若MN为圆C在X轴上截和的弦,设|AM|=l1,|AN|=l2,∠MAN=α.
已知:圆C过定点A(0,p),圆心C在抛物线x2=2py上运动,若MN为圆C在X轴上截和的弦,设|AM|=l1,|AN|=l2,∠MAN=α.(1)当点C运动时,|MN|是否变化?写出并证明你的结论;
(2)求
| l1 |
| l2 |
| l2 |
| l1 |
分析:(1)先设出圆的方程,求出M,N两点的坐标表示出|MN|即可发现|MN|的取值是否变化.
(2)先利用三角形的面积公式求出l1l2=
,再利用余弦定理求出l12+l22的表达式.代入
+
整理为关于θ的函数,利用θ的范围来求
+
的最大值和此时圆C的方程即可.
(2)先利用三角形的面积公式求出l1l2=
| 2p2 |
| sinθ |
| l1 |
| l2 |
| l2 |
| l1 |
| l1 |
| l2 |
| l2 |
| l1 |
解答: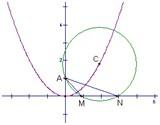 解:(1):由题意得:⊙C的方程(x-x0)2+(y-y0)2=x02+(y0-1)2.
解:(1):由题意得:⊙C的方程(x-x0)2+(y-y0)2=x02+(y0-1)2.
把y=0和x02=2py0代入整理得x2-2x0x+x02+xp2=0.
解之得方程的两根分为
x1=x0-p,x2=x0+p.∴|MN|=|x1-x2|=2P.
∴点C运动时,|MN|不会变化,|MN|=2P(定值)
(2)设∠MAN=θ
∵S△AMN=
l1•l2• sinθ=
|OA||MN|=p2,∴l1l2=
∵l12+l22-2l1l2cosθ=4P2,∴l12+l22=4P2+
cosθ=4P2(1+ctgθ).
∴
+
=
=
=2
sin(θ+
).
∵只有当C在O点处时,θ为直径上圆周角,其他时候都是劣弧上的圆周角.
∴0<θ≤
,
故当θ=
时,原式有最大值2
.
∵∠MAN=
,∴∠MCN=2∠MAN=
∴y0=P,x0=±
P,r=
P.
所求圆的方程为(x-
p)2+(y-p)2=2p2或((x+
p)2+(y-p)2=2p2.
 解:(1):由题意得:⊙C的方程(x-x0)2+(y-y0)2=x02+(y0-1)2.
解:(1):由题意得:⊙C的方程(x-x0)2+(y-y0)2=x02+(y0-1)2.把y=0和x02=2py0代入整理得x2-2x0x+x02+xp2=0.
解之得方程的两根分为
x1=x0-p,x2=x0+p.∴|MN|=|x1-x2|=2P.
∴点C运动时,|MN|不会变化,|MN|=2P(定值)
(2)设∠MAN=θ
∵S△AMN=
| 1 |
| 2 |
| 1 |
| 2 |
| 2p2 |
| sinθ |
∵l12+l22-2l1l2cosθ=4P2,∴l12+l22=4P2+
| 4P2 |
| sinθ |
∴
| l2 |
| l1 |
| l1 |
| l2 |
| l12+l22 |
| l1l2 |
| 4P2(1+ctgθ)sinθ |
| 2P2 |
| 2 |
| π |
| 4 |
∵只有当C在O点处时,θ为直径上圆周角,其他时候都是劣弧上的圆周角.
∴0<θ≤
| π |
| 2 |
故当θ=
| π |
| 4 |
| 2 |
∵∠MAN=
| π |
| 4 |
| π |
| 2 |
| 2 |
| 2 |
所求圆的方程为(x-
| 2 |
| 2 |
点评:本题是对圆与抛物线以及余弦定理,三角形面积公式等知识的综合考查,做这一类型题,读题很关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
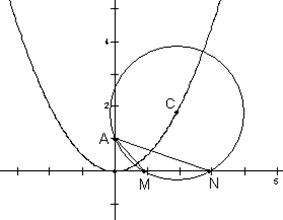

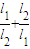 的最大值,并求取得这个最大值时α的值和此时圆C的方程.
的最大值,并求取得这个最大值时α的值和此时圆C的方程.
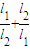 的最大值,并求取得这个最大值时α的值和此时圆C的方程.
的最大值,并求取得这个最大值时α的值和此时圆C的方程.