题目内容
已知两条直线l1:x+my+6=0,l2:(m-2)x+3y+2m=0,问:当m为何值时,l1与l2(i)相交;
(ii)平行;
(iii)重合.
分析:(i)当m≠0分别表示出两直线的斜截式,当斜率不相等时,直线相交;
(ii)当斜率相等但截距不相等时,两直线平行;
(iii)当斜率相等且截距相等时,两直线重合;而m=0,得到两直线相交.综合上面可得相应m的范围.
(ii)当斜率相等但截距不相等时,两直线平行;
(iii)当斜率相等且截距相等时,两直线重合;而m=0,得到两直线相交.综合上面可得相应m的范围.
解答:解:(1)若m=0时,l1:x=-6,l2:2x-3y=0,此时l1与l2相交;
(2)若m≠0,由
=
有m=-1或m=3,
由
=
有m=±3;
故(i)当m≠-1且m≠3时,
≠
,l1与l2相交;
(ii)当m=-1时,
=
≠
,l1与l2平行;
(iii)当m=3时
=
=
,l1与l2重合.
(2)若m≠0,由
| m-2 |
| 1 |
| 3 |
| m |
由
| 3 |
| m |
| 2m |
| 6 |
故(i)当m≠-1且m≠3时,
| m-2 |
| 1 |
| 3 |
| m |
(ii)当m=-1时,
| m-2 |
| 1 |
| 3 |
| m |
| 2m |
| 6 |
(iii)当m=3时
| m-2 |
| 1 |
| 3 |
| m |
| 2m |
| 6 |
点评:此题为中档题,要求学生会利用代数的方法研究图象的位置关系,做此题时应采用分类讨论的方法分情况得到所求的范围.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
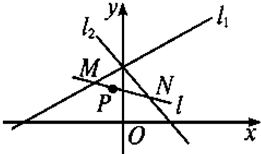 如图,已知两条直线l1:x-3y+12=0,l2:3x+y-4=0,过定点P(-1,2)作一条直线l,分别与l1,l2交于M、N两点,若P点恰好是MN的中点,求直线l的方程.
如图,已知两条直线l1:x-3y+12=0,l2:3x+y-4=0,过定点P(-1,2)作一条直线l,分别与l1,l2交于M、N两点,若P点恰好是MN的中点,求直线l的方程.