题目内容
已知数列{an}是各项均为正数的等比数列，若a2=2，2a3+a4=16，则an= ．
分析：利用数列{an}是各项均为正数的等比数列，a2=2，2a3+a4=16，求出公比与首项，即可求得数列的通项．
解答：解：设等比数列的公比为q，则
∵等比数列{an}中，a2=2，2a3+a4=16，
∴4q+2q2=16，
∴q2+2q-8=0，
∵q＞0，
∴q=2，
∵a2=2，
∴a1=1，
∴an=2n-1．
故答案为：2n-1．
∵等比数列{an}中，a2=2，2a3+a4=16，
∴4q+2q2=16，
∴q2+2q-8=0，
∵q＞0，
∴q=2，
∵a2=2，
∴a1=1，
∴an=2n-1．
故答案为：2n-1．
点评：本题考查等比数列的通项，考查学生的计算能力，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
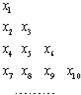若一个数列各项取倒数后按原来的顺序构成等差数列，则称这个数列为调和数列．已知数列{an}是调和数列，对于各项都是正数的数列{xn}，满足
若一个数列各项取倒数后按原来的顺序构成等差数列，则称这个数列为调和数列．已知数列{an}是调和数列，对于各项都是正数的数列{xn}，满足
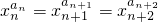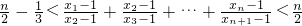（n∈N*）．
．
（n∈N*）．
．
（n∈N*）．
．