题目内容
椭圆 的左、右焦点分别是F1,F2,过F1的直线l与椭圆C相交于A,B两点,且|AF2|,|AB|,|BF2|成等差数列.
的左、右焦点分别是F1,F2,过F1的直线l与椭圆C相交于A,B两点,且|AF2|,|AB|,|BF2|成等差数列.
(1)求证: ;
;
(2)若直线l的斜率为1,且点(0,-1)在椭圆C上,求椭圆C的方程.
(1)证明:由题设,∵|AF2|,|AB|,|BF2|成等差数列,∴2|AB|=|AF2|+|BF2|,
由椭圆定义|AB|+|AF2|+|BF2|=4a,
所以, .
.
(2)解:由点(0,-1)在椭圆C上,可设椭圆C的方程为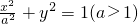 ,
,
设A(x1,y1),B(x2,y2),F1(-c,0),l:x=y-c,代入椭圆C的方程,整理得(a2+1)y2-2cy-1=0,(*)
则 =
= ,
,
于是有 ,
,
解得 ,故椭圆C的方程为
,故椭圆C的方程为 .
.
分析:(1)利用等差数列的性质,结合椭圆的定义,即可证得结论;
(2)设出椭圆的方程,直线方程与椭圆方程联立,计算|AB|,利用(1)的结论,即可求得椭圆的标准方程.
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查弦长的计算,解题的关键是利用椭圆的定义求弦长.
由椭圆定义|AB|+|AF2|+|BF2|=4a,
所以,
 .
.(2)解:由点(0,-1)在椭圆C上,可设椭圆C的方程为
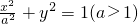 ,
,设A(x1,y1),B(x2,y2),F1(-c,0),l:x=y-c,代入椭圆C的方程,整理得(a2+1)y2-2cy-1=0,(*)
则
 =
= ,
,于是有
 ,
,解得
 ,故椭圆C的方程为
,故椭圆C的方程为 .
.分析:(1)利用等差数列的性质,结合椭圆的定义,即可证得结论;
(2)设出椭圆的方程,直线方程与椭圆方程联立,计算|AB|,利用(1)的结论,即可求得椭圆的标准方程.
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查弦长的计算,解题的关键是利用椭圆的定义求弦长.

练习册系列答案
相关题目
 的左、右焦点分别为F1、F2,其中F2也是抛物线
的左、右焦点分别为F1、F2,其中F2也是抛物线 的焦点,M是C1与C2在第一象限的交点,且
的焦点,M是C1与C2在第一象限的交点,且
 上,求直线AC的方程。
上,求直线AC的方程。