题目内容
定义在(-1,1)上的奇函数f(x)=| x+m | x2+nx+1 |
分析:由题意函数f(x)是定义在(-1,1)上的奇函数,利用奇函数若在0出有定义则f(0)=0,解出m的值,在利用奇函数的定义得到f(-1)=-f(1),即可解出n.
解答:解:因为函数f(x)是定义在(-1,1)上的奇函数,所以必定有f(0)=
=0?m=0,
此时f(x)=
,
函数f(x)是定义在(-1,1)上的奇函数得到f(-x)=-f(x),
即
=
?n=0.
故答案为:m=0,n=0.
| m |
| 1 |
此时f(x)=
| x |
| x2+nx+1 |
函数f(x)是定义在(-1,1)上的奇函数得到f(-x)=-f(x),
即
| x+m |
| x2+nx+1 |
| (-x)+m |
| (-x)2+n(-x)+1 |
故答案为:m=0,n=0.
点评:此题考查了奇函数若在0出有定义则f(0)=0这一结论,还考查了奇函数的定义及求解一元一次方程.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 是定义在(-1,1)的奇函数,且f(
是定义在(-1,1)的奇函数,且f( )=
)= .
.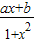 是定义在(-1,1)的奇函数,且f(
是定义在(-1,1)的奇函数,且f( )=
)= .
.