题目内容
直线l过抛物线y2=2px(p>0)的焦点F,且交抛物线于P,Q两点,由P,Q分别向准线引垂线PR、QS,垂足分别为R,S,如果|PF|=a,|QF|=b,M为RS的中点,则|MF|=
- A.a+b
- B.

- C.

- D.

C
分析:分PQ⊥x轴,和PQ与x轴不垂直两种情况,利用抛物线的定义、直角三角形斜边中线的性质、矩形的性质和勾股定理即可得出.
解答:①PQ与x轴不垂直时,如图所示,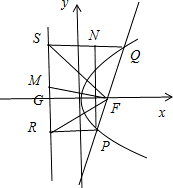
由抛物线的定义可得|QF|=|QS|,|PF|=|PR|.
∴∠QFS=∠QSF,∠PFR=∠PRF,
由题意可得QS∥FG∥PR,∴∠SFG=∠QSF,∠RFG=∠PRF.
∴∠SFG+∠RFG=90°,∴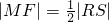 .
.
过点P作PN⊥QS交于点N,则|PN|=|RS|.
在Rt△PQN中,|PN|=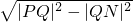 =
=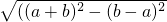 =2
=2 .
.
∴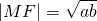 .
.
②当PQ⊥x轴时,也可|MF|=p=a=b= .
.
综上可知:|MF|= .
.
故选C.
点评:熟练掌握抛物线的定义、直角三角形斜边中线的性质、矩形的性质和勾股定理、分类讨论的数学方法是解题的关键.
分析:分PQ⊥x轴,和PQ与x轴不垂直两种情况,利用抛物线的定义、直角三角形斜边中线的性质、矩形的性质和勾股定理即可得出.
解答:①PQ与x轴不垂直时,如图所示,

由抛物线的定义可得|QF|=|QS|,|PF|=|PR|.
∴∠QFS=∠QSF,∠PFR=∠PRF,
由题意可得QS∥FG∥PR,∴∠SFG=∠QSF,∠RFG=∠PRF.
∴∠SFG+∠RFG=90°,∴
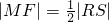 .
.过点P作PN⊥QS交于点N,则|PN|=|RS|.
在Rt△PQN中,|PN|=
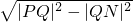 =
=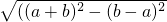 =2
=2 .
.∴
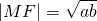 .
.②当PQ⊥x轴时,也可|MF|=p=a=b=
 .
.综上可知:|MF|=
 .
.故选C.
点评:熟练掌握抛物线的定义、直角三角形斜边中线的性质、矩形的性质和勾股定理、分类讨论的数学方法是解题的关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
设斜率为2的直线l过抛物线y2=ax(a≠0)的焦点F,且和y轴交于点A,若△OAF(O为坐标原点)的面积为4,则抛物线方程为( )
| A、y2=±4x | B、y2=4x | C、y2=±8x | D、y2=8x |
已知斜率为2的直线l过抛物线y2=ax的焦点F,且与y轴相交于点A,若△OAF(O为坐标原点)的面积为4,则抛物线方程为( )
| A、y2=4x | B、y2=8x | C、y2=4x或y2=-4x | D、y2=8x或y2=-8x |