题目内容
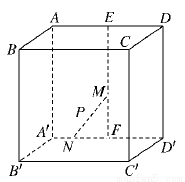
 在棱长为4的正方体ABCD-A1B1C1D1中,O是正方形A1B1C1D1的中心,点P在棱CC1上,且CC1=4CP.
在棱长为4的正方体ABCD-A1B1C1D1中,O是正方形A1B1C1D1的中心,点P在棱CC1上,且CC1=4CP.(Ⅰ)求直线AP与平面BCC1B1所成的角的大小(结果用反三角函数值表示);
(Ⅱ)设O点在平面D1AP上的射影是H,求证:D1H⊥AP;
(Ⅲ)求点P到平面ABD1的距离.
分析:本题宜建立空间坐标系,用空间向量来解决求线面角证线线垂直,求点到面 距离.
(Ⅰ)由题设条件,连接AC,即可得出AP与平面BCC1B1所成的角为∠PAC,求出线的方向向量与面的法向量,用公式求出线面角的正弦.
(Ⅱ)由图形及题设条件可以证得AP⊥面D1OH,由线面垂直证得母线线垂直,求出两线.
(Ⅲ)用向量法求点到面的距离,求线段对应的向量在面的法向量的投影的长度即可.
(Ⅰ)由题设条件,连接AC,即可得出AP与平面BCC1B1所成的角为∠PAC,求出线的方向向量与面的法向量,用公式求出线面角的正弦.
(Ⅱ)由图形及题设条件可以证得AP⊥面D1OH,由线面垂直证得母线线垂直,求出两线.
(Ⅲ)用向量法求点到面的距离,求线段对应的向量在面的法向量的投影的长度即可.
解答: 解:建立如图的空间坐标系,由已知D(0,0,0),A(4,0,0),C(0,4,0),
解:建立如图的空间坐标系,由已知D(0,0,0),A(4,0,0),C(0,4,0),
D(0,0,4),B(4,4,0)
(1)如图,连接PB,由正方体的性质知∠APB即为所求的线面角,∵CC1=4CP∴CP=1,由勾股定理知BP=
,
∴tan∠APB=
=
=
∴∠APB=arctan
(2)证明:由已知OH⊥面APD1,∴OH⊥AP,
连接B1D1,由于O是上底面的中心,故O∈B1D1,
由正体的性质知B1D1⊥面AC1,
又AP?面AC1,
∴B1D1⊥AP
又B1D1∩OH=0
∴AP⊥面D1OH,
∴D1H⊥AP
(3)如图
=(0,4,0),
=(-4,0,4)
=(-4,4,1)
令面ABD1的法向量为
=(x,y,z)
故有
,即
令x=1,则z=1,故
=(1,0,1)
故点P到面面ABD1的距离d=
=
点P到面面ABD1的距离为
 解:建立如图的空间坐标系,由已知D(0,0,0),A(4,0,0),C(0,4,0),
解:建立如图的空间坐标系,由已知D(0,0,0),A(4,0,0),C(0,4,0),D(0,0,4),B(4,4,0)
(1)如图,连接PB,由正方体的性质知∠APB即为所求的线面角,∵CC1=4CP∴CP=1,由勾股定理知BP=
| 17 |
∴tan∠APB=
| AB |
| PB |
| 4 | ||
|
4
| ||
| 17 |
∴∠APB=arctan
| 4 |
| 17 |
| 17 |
(2)证明:由已知OH⊥面APD1,∴OH⊥AP,
连接B1D1,由于O是上底面的中心,故O∈B1D1,
由正体的性质知B1D1⊥面AC1,
又AP?面AC1,
∴B1D1⊥AP
又B1D1∩OH=0
∴AP⊥面D1OH,
∴D1H⊥AP
(3)如图
| AB |
| AD 1 |
| AP |
令面ABD1的法向量为
| n |
故有
|
|
令x=1,则z=1,故
| n |
故点P到面面ABD1的距离d=
| 3 | ||
|
3
| ||
| 2 |
点P到面面ABD1的距离为
| 3 |
| 2 |
| 2 |
点评:本考点是立体几何,对三个问题其中前两个问题用几何法证明较易,故采用了几何法,而第三个问题点到面的垂线段不易做出,故采用了向量法求点到面的距离,在做题时应根据题目的条件灵活选用解题的方法.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
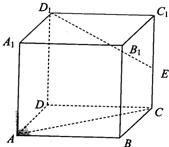 如图所示,在棱长为4的正方体ABCD-A1B1C1D1中,点E是棱CC1的中点.
如图所示,在棱长为4的正方体ABCD-A1B1C1D1中,点E是棱CC1的中点.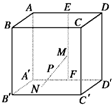 如图,在棱长为4的正方体ABCD-A′B′C′D′中,E、F分别是AD、A′D′的中点,长为2的线段MN的一个端点M在线段EF上运动,另一个端点N在底面A′B′C′D′上运动,则线段MN的中点P的轨迹(曲面)与二面角A-A′D′-B′所围成的几何体的体积为( )
如图,在棱长为4的正方体ABCD-A′B′C′D′中,E、F分别是AD、A′D′的中点,长为2的线段MN的一个端点M在线段EF上运动,另一个端点N在底面A′B′C′D′上运动,则线段MN的中点P的轨迹(曲面)与二面角A-A′D′-B′所围成的几何体的体积为( ) 在棱长为4的正方体ABCD-A1B1C1D1中,点E、F分别在棱AA1和AB上,且C1E⊥EF,则|AF|的最大值为( )
在棱长为4的正方体ABCD-A1B1C1D1中,点E、F分别在棱AA1和AB上,且C1E⊥EF,则|AF|的最大值为( )