题目内容
19世纪德国数学家狄利克雷（1805-1859）定义了一个“奇怪的函数”--狄利克雷函数：f（x）=
，则该函数为 函数（选填：奇、偶、非奇非偶、既奇又偶）
|
分析：该题是分段函数，需注意x为有理数，则-x也为有理数，x为无理数，则-x也为无理数，最后根据奇偶性的定义进行判断即可．
解答：解：∵f（x）=
，
①当x∈Q时，则-x∈Q，
∴f（-x）=f（x）=1，
②当x∈CRQ，则-x∈CRQ，
∴f（-x）=f（x）=0，
综合①②，对于任意x∈R，都有f（-x）=f（x），故该函数为偶函数．
故答案为：偶．
|
①当x∈Q时，则-x∈Q，
∴f（-x）=f（x）=1，
②当x∈CRQ，则-x∈CRQ，
∴f（-x）=f（x）=0，
综合①②，对于任意x∈R，都有f（-x）=f（x），故该函数为偶函数．
故答案为：偶．
点评：本题综合考查了狄氏函数的奇偶性判定，常用奇偶性的定义判断函数的奇偶性，同时考查了分析问题的能力，属于基础题．
练习册系列答案
相关题目
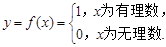，这个函数后来被称为狄利克雷函数。下面对此函数性质的描述中不正确的是：（ ）
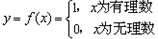，这个函数后来被称为狄利克雷函数。下面对此函数性质的描述中不正确的是