题目内容
【题目】设圆![]() 的圆心为A,直线l过点B(1,0)且与x轴不重合,l交圆A于C,D两点,过B作AC的平行线交AD于点E.
的圆心为A,直线l过点B(1,0)且与x轴不重合,l交圆A于C,D两点,过B作AC的平行线交AD于点E.
(I)证明![]() 为定值,并写出点E的轨迹方程;
为定值,并写出点E的轨迹方程;
(II)设点E的轨迹为曲线C1,直线l交C1于M,N两点,过B且与l垂直的直线与圆A交于P,Q两点,求四边形MPNQ面积的取值范围.
【答案】(Ⅰ)答案见解析;(Ⅱ)![]() .
.
【解析】
试题(Ⅰ)利用椭圆定义求方程;(Ⅱ)把面积表示为关于斜率k的函数,再求最值.
试题解析:(Ⅰ)因为![]() ,
,![]() ,故
,故![]() ,
,
所以![]() ,故
,故![]() .
.
又圆![]() 的标准方程为
的标准方程为![]() ,从而
,从而![]() ,所以
,所以![]() .
.
由题设得![]() ,
,![]() ,
,![]() ,由椭圆定义可得点
,由椭圆定义可得点![]() 的轨迹方程为:
的轨迹方程为:
![]() (
(![]() ).
).
(Ⅱ)当![]() 与
与![]() 轴不垂直时,设
轴不垂直时,设![]() 的方程为
的方程为![]() ,
,![]() ,
,![]() .
.
由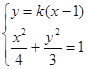 得
得![]() .
.
则![]() ,
,![]() .
.
所以![]() .
.
过点![]() 且与
且与![]() 垂直的直线
垂直的直线![]() :
:![]() ,
,![]() 到
到![]() 的距离为
的距离为![]() ,所以
,所以
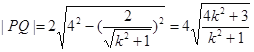 .故四边形
.故四边形![]() 的面积
的面积
![]() .
.
可得当![]() 与
与![]() 轴不垂直时,四边形
轴不垂直时,四边形![]() 面积的取值范围为
面积的取值范围为![]() .
.
当![]() 与
与![]() 轴垂直时,其方程为
轴垂直时,其方程为![]() ,
,![]() ,
,![]() ,四边形
,四边形![]() 的面积为12.
的面积为12.
综上,四边形![]() 面积的取值范围为
面积的取值范围为![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
