题目内容
3.已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左、右顶点是双曲线$\frac{x^2}{3}-{y^2}=1$的顶点,且椭圆的上顶点到双曲线的渐近线的距离为$\frac{{\sqrt{3}}}{2}$,(Ⅰ)求椭圆的方程;
(Ⅱ)是否存在同时满足下列两个条件的直线l:①与双曲线相交于Q1、Q2两点,且$\overrightarrow{O{Q_1}}•\overrightarrow{O{Q_2}}=-5$,②与相交于M1、M2两点,且$|{{M_1}{M_2}}|=\sqrt{10}$.若存在,求出直线l的方程,若不存在,说明理由.
分析 (Ⅰ)由题意求得a2=3,再由椭圆的上顶点到双曲线的渐近线的距离为$\frac{{\sqrt{3}}}{2}$求得b=1,则椭圆的方程可求;
(Ⅱ)假设存在直线满足条件,设出直线l的方程为y=kx+m,代入双曲线方程化为关于x的一元二次方程,得到m与k的关系,再利用根与系数关系结合$\overrightarrow{O{Q_1}}•\overrightarrow{O{Q_2}}=-5$得到m2=1-9k2.再把直线和椭圆联立,由判别式大于0求得3k2+1>m2,进一步求得k的范围,利用根与系数的关系得到M1、M2两点的横坐标的和与积,代入弦长公式即可求得k的值,得到m的值,则直线l的方程可求.
解答 解:(Ⅰ)由题意可知:a2=3,
又椭圆的上顶点为(0,b),双曲线的渐近线为:$y=±\frac{\sqrt{3}}{3}x$,即$x±\sqrt{3}y=0$,
由点到直线的距离公式有:$\frac{\sqrt{3}}{2}=\frac{|±\sqrt{3}b|}{2}$,即b=1,
∴椭圆的方程为:$\frac{x^2}{3}+{y^2}=1$;
(Ⅱ)假设存在直线满足条件,则它的斜率一定存在.
设直线l的方程为y=kx+m,代入$\frac{x^2}{3}-{y^2}=1$,消去y并整理得:(1-3k2)x2-6kmx-3m2-3=0.
则:$\left\{\begin{array}{l}1-3{k^2}≠0\\ 36{k^2}{m^2}-4(1-3{k^2})(-3{m^2}-3)>0\end{array}\right.$,即$\left\{\begin{array}{l}{1-3{k}^{2}≠0}\\{{m}^{2}+1>3{k}^{2}}\end{array}\right.$,…①
设Q1(x1,y1)、Q2(x2,y2),则有:${x_1}+{x_2}=\frac{6km}{{1-3{k^2}}}$,${x_1}•{x_2}=\frac{{-3{m^2}-3}}{{1-3{k^2}}}$.
又$\overrightarrow{O{Q_1}}•\overrightarrow{O{Q_2}}={x_1}{x_2}+{y_1}{y_2}$=x1x2+(kx1+m)(kx2+m)=$(1+{k^2}){x_1}{x_2}+km({x_1}+{x_2})+{m^2}$,且$\overrightarrow{O{Q_1}}•\overrightarrow{O{Q_2}}=-5$,
∴$\frac{1}{{1-3{k^2}}}[(1+{k^2})(-3{m^2}-3)+6{k^2}{m^2}+{m^2}(1-3{k^2})]=-5$,得m2=1-9k2. …②
将y=kx+m代入$\frac{x^2}{3}+{y^2}=1$,消去y并整理得:(1+3k2)x2+6kmx+3m2-3=0,
则△=36k2m2-4(1+3k2)(3m2-3)>0,即3k2+1>m2,…③
由①②③有:$0<{k^2}≤\frac{1}{9}$.
设M1(x3,y3)、M2(x4,y4),则有:${x_3}+{x_4}=\frac{-6kb}{{1+3{k^2}}}$,${x_3}•{x_4}=\frac{{3{b^2}-3}}{{1+3{k^2}}}$.
∴$|{{M_1}{M_2}}|=\sqrt{1+{k^2}}•\sqrt{\frac{{36{k^2}{b^2}-4(3{b^2}-3)(1+3{k^2})}}{{{{(1+3{k^2})}^2}}}}$=$\sqrt{1+{k^2}}•\sqrt{\frac{{-4(3{b^2}-3-9{k^2})}}{{{{(1+3{k^2})}^2}}}}$,
又b2=1-9k2,代入上式得:$|{{M_1}{M_2}}|=\sqrt{1+{k^2}}•\sqrt{\frac{{144{k^2}}}{{{{(1+3{k^2})}^2}}}}$=$\frac{12|k|}{1+3{k}^{2}}\sqrt{1+{k}^{2}}$,
由$|{{M_1}{M_2}}|=\sqrt{10}$,得$\frac{12|k|}{1+3{k}^{2}}\sqrt{1+{k}^{2}}=\sqrt{10}$,解得$k=±\frac{1}{3}$满足条件.
代入b2=1-9k2,可求得b=0,
故存在满足条件的直线l,其方程为$y=±\frac{1}{3}x$.
点评 本题考查椭圆方程的求法,考查了直线与椭圆的位置关系的应用,直线与曲线联立,根据方程的根与系数的关系求解,是处理这类问题的最为常用的方法,但圆锥曲线的特点是计算量比较大,要求考试具备较强的运算推理的能力,是压轴题.

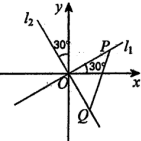 如图,两条过原点.D的直线l1,l2分别与x轴、y轴正方向成30°的角,点P(x1,y1)在直线l1上运动,点Q(x2,y2)在直线l2上运动,且线段PQ的长度为2.
如图,两条过原点.D的直线l1,l2分别与x轴、y轴正方向成30°的角,点P(x1,y1)在直线l1上运动,点Q(x2,y2)在直线l2上运动,且线段PQ的长度为2.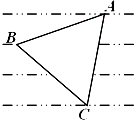 如图所示,某服装设计师要在一块条形布料上画一个等边△ABC作为点缀,使A、B、C三点分别落在条形布料的线条上,已知条形布料相邻横线间的距离为3厘米,则等边△ABC的边长应为2$\sqrt{21}$厘米.
如图所示,某服装设计师要在一块条形布料上画一个等边△ABC作为点缀,使A、B、C三点分别落在条形布料的线条上,已知条形布料相邻横线间的距离为3厘米,则等边△ABC的边长应为2$\sqrt{21}$厘米.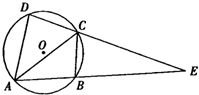 如图所示,四边形ABCD的外接圆为圆O,线段AB与线段DC的延长线交于点E,$\frac{AD}{DE}$=$\frac{1}{3}$.
如图所示,四边形ABCD的外接圆为圆O,线段AB与线段DC的延长线交于点E,$\frac{AD}{DE}$=$\frac{1}{3}$.