Question

f(x)=x2-|x-

1

4

|的零点的个数为

 

．

Answer 1

分析：本题即求函数y=x² 的图象和y=|x-

1

4

|的图象的交点个数，数形结合可得结论．

解答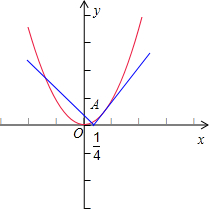：解：f(x)=x2-|x-

1

4

|的零点的个数，
即函数y=x² 的图象和y=|x-

1

4

|=

-x+ 1 4  ，x＜ 1 4 x- 1 4  ，x≥ 1 4

 的图象的交点的个数，如图所示：
显然，函数y=x² 的图象和射线y=-x+

1

4

（x＜

1

4

）有2个交点．
再由

y=x2 y=-x+ 1 4

可得x²-x+

1

4

=0．
由于判别式△=1-1=0，故y=x² y=x-

1

4

（x≥

1

4

）只有一个交点．
综上可得，函数y=x² 的图象和y=|x-

1

4

|的图象的交点的个为3，
故答案为：3．

点评：本题主要考查函数的零点与方程的根的关系，体现了转化以及数形结合的数学思想，属于基础题．