题目内容
若(1+x)6(1-2x)5=a0+a1x+a2x2+…+a11x11.求:(1)a1+a2+a3+…+a11;
(2)a0+a2+a4+…+a10.
解:(1)(1+x)6(1-2x)5=a0+a1x+a2x2+…+a11x11.令x=1,得
a0+a1+a2+…+a11=-26. ①
又a0=1,
所以a1+a2+…+a11=-26-1=-65.
(2)再令x=-1,得
a0-a1+a2-a3+…-a11=0. ②
①+②得a0+a2+…+a10=![]() (-26+0)=-32.
(-26+0)=-32.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
下列命题中正确的有
①设有一个回归方程 =2—3x,变量x增加一个单位时,y平均增加3个单位;
=2—3x,变量x增加一个单位时,y平均增加3个单位;
②命题P:“ ”的否定
”的否定 P:“
P:“ ”;
”;
③设随机变量X服从正态分布N(0,1),若P(X>1)=p,则P(-1<X<0)= -p;
-p;
④在一个2×2列联表中,由计算得k2=6.679,则有99%的把握确认这两个变量间有关系.
A.1个 B.2个 C.3个 D.4个
本题可以参考独立性检验临界值表
|
P(K2≥k) |
0.5 |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
|
k |
0.455 |
0.708 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.535 |
7.879 |
10.828 |
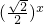 -1,若在区间(-2,6)内的关于x的方程f(x)-logga(x+2)=0(a>0且a≠1)恰有4个不同的实数根,则实数a的取值范围是
-1,若在区间(-2,6)内的关于x的方程f(x)-logga(x+2)=0(a>0且a≠1)恰有4个不同的实数根,则实数a的取值范围是 ,1)
,1)