Question

过点P(2,1)作直线l,与x、y轴的正半轴分别交于A、B两点,要使|PA|·|PB|最小,求直线l的方程.

Answer 1

x+y-3=0.

解析:

解法一:设所求直线l的方程为y-1=k(x-2)(k＜0).

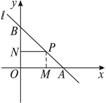
则点A、B的坐标分别为(,0)和(0,1-2k).

|PA|=

=-,|PB|=.

所以|PA|·|PB|=.

设=m(*).则2k²+mk+2=0.

因为Δ=m²-16≥0,

所以m≥4或m≤-4.

因为m＞0,所以m最小值为4.代入(*)式得

2k²+4k+2=0,即k=-1.

所以所求直线的方程为y-1=-(x-2),

即x+y-3=0.

解法二:由条件k＜0,且由解法一得

|PA|·|PB|=.

此时,即k²=1.

因为k＜0,所以k=-1.

故所求l的方程为y-1=-(x-2),即x+y-3=0.

解法三:设直线l的倾斜角为α,则

|PA|=,.

所以|PA|·|PB|=.

因为90°＜α＜180°,

所以当2α=270°,即α=135°时,|PA|·|PB|有最小值.

所以l的方程为y-1=-(x-2),即x+y-3=0.