题目内容
已知数列{an}和{bn}满足a1=b1,且对任意n∈N*都有an+bn=1,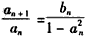 ,
,
(Ⅰ)求数列{an}和{bn}的通项公式;
(Ⅱ)证明: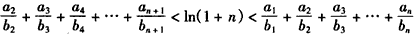 。
。
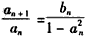 ,
,(Ⅰ)求数列{an}和{bn}的通项公式;
(Ⅱ)证明:
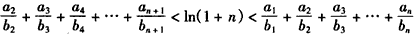 。
。 (Ⅰ)解:∵对任意n∈N*都有an+bn=1,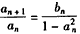 ,
,
∴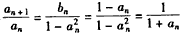 ,
,
∴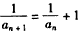 ,即
,即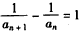 ,
,
∴数列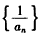 是首项为
是首项为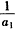 ,公差为1的等差数列,
,公差为1的等差数列,
∵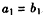 ,且
,且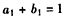 ,
,
∴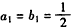 ,
,
∴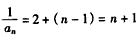 ,
,
∴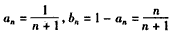 。
。
(Ⅱ) 证明:∵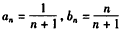 ,
,
∴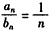 ,
,
∴所证不等式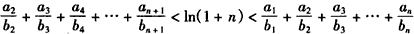 ,
,
即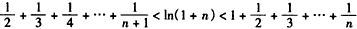 ,
,
①先证右边不等式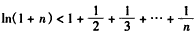 ,
,
令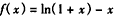 ,
,
则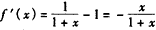 ,
,
当x>0时,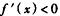 ,
,
所以函数f(x)在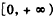 上单调递减,
上单调递减,
∴当x>0时,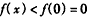 ,即
,即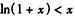 ,
,
分别取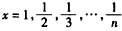 ,
,
得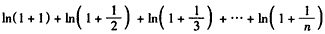
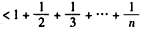 ,
,
即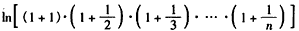
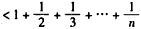 ,
,
也即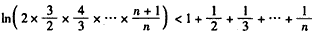 ,
,
即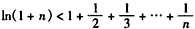 ,
,
②再证左边不等式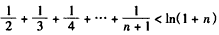 ,
,
令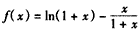 ,
,
则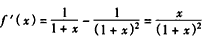 ,
,
当x>0时,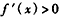 ,
,
所以函数f(x)在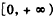 上单调递增,
上单调递增,
所以,当x>0时,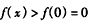 ,即
,即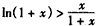 ,
,
分别取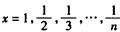 ,
,
得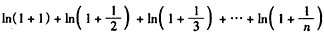
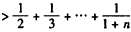 ,
,
即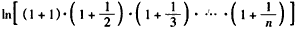
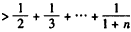 ,
,
也即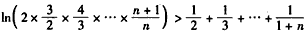 ,
,
即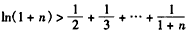 ,
,
∴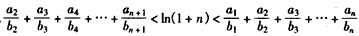 。
。
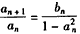 ,
,∴
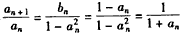 ,
,∴
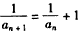 ,即
,即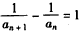 ,
,∴数列
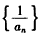 是首项为
是首项为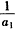 ,公差为1的等差数列,
,公差为1的等差数列,∵
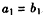 ,且
,且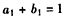 ,
,∴
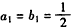 ,
,∴
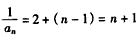 ,
,∴
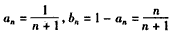 。
。(Ⅱ) 证明:∵
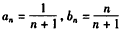 ,
,∴
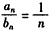 ,
,∴所证不等式
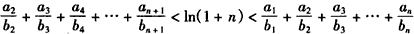 ,
,即
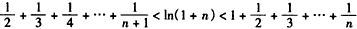 ,
,①先证右边不等式
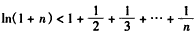 ,
,令
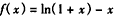 ,
,则
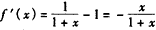 ,
,当x>0时,
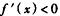 ,
,所以函数f(x)在
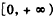 上单调递减,
上单调递减,∴当x>0时,
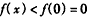 ,即
,即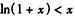 ,
,分别取
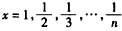 ,
,得
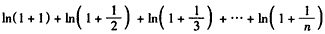
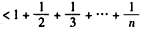 ,
,即
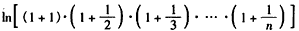
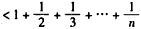 ,
,也即
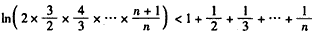 ,
,即
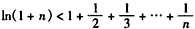 ,
,②再证左边不等式
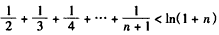 ,
,令
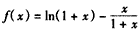 ,
,则
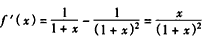 ,
,当x>0时,
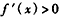 ,
,所以函数f(x)在
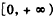 上单调递增,
上单调递增,所以,当x>0时,
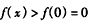 ,即
,即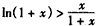 ,
,分别取
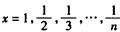 ,
,得
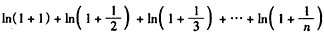
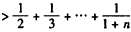 ,
,即
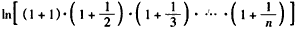
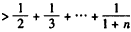 ,
,也即
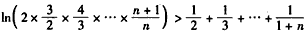 ,
,即
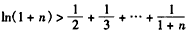 ,
,∴
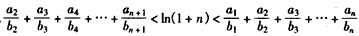 。
。
练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目