题目内容
公差不为零的等差数列 的前
的前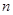 项和为
项和为 .若
.若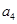 是
是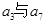 的等比中项,
的等比中项, 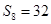 ,则
,则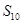 等于()
等于()
| A. 18 | B. 24 | C. 60 | D. 90 |
C
解析试题分析:解:∵a4是a3与a7的等比中项,,∴a42=a3a7,,即(a1+3d)2=(a1+2d)(a1+6d),,整理得2a1+3d=0,①,又∵S8=8a1+ d=32,整理得2a1+7d=8,②由①②联立,解得d=2,a1=-3,∴S10=10a1+
d=32,整理得2a1+7d=8,②由①②联立,解得d=2,a1=-3,∴S10=10a1+ d=60,故选C.
d=60,故选C.
考点:等差数列的通项公式
点评:本题考查了等差数列的通项公式、前n项和公式和等比中项的定义,比较简单.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
已知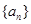 为等差数列,其前
为等差数列,其前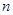 项和为
项和为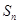 ,若
,若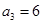 ,
,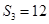 ,则公差
,则公差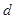 等于( )
等于( )
A. | B.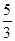 | C. | D. |
如果等差数列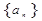 中,
中, ,那么
,那么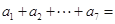 ( )
( )
| A.14 | B.21 | C.28 | D.35 |
等差数列 的前
的前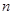 项和为
项和为 的值( )
的值( )
| A.18 | B.20 | C.21 | D.22 |
已知等差数列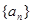 中,
中,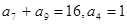 ,则
,则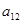 的值是 ( )
的值是 ( )
| A.30 | B.15 | C.31 | D.64 |
已知数列{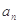 }满足
}满足 ,其中
,其中 为实常数,则数列{
为实常数,则数列{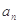 }( )
}( )
| A.不可能是等差数列,也不可能是等比数列 |
| B.不可能是等差数列,但可能是等比数列 |
| C.可能是等差数列,但不可能是等比数列 |
| D.可能是等差数列,也可能是等比数列 |
等差数列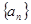 中,
中, 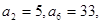 则
则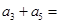 ( )
( )
A.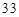 | B.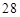 | C.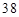 | D.52 |