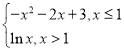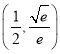题目内容
【题目】已知椭圆![]() 经过
经过![]() 两点,
两点,![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的标准方程;
的标准方程;
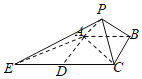
(2)设动直线![]() 与椭圆
与椭圆![]() 有且仅有一个公共点,且与圆
有且仅有一个公共点,且与圆![]() 相交于
相交于![]() 两点,试问直线
两点,试问直线![]() 与
与![]() 的斜率之积
的斜率之积![]() 是否为定值?若是,求出该定值;若不是,说明理由.
是否为定值?若是,求出该定值;若不是,说明理由.
【答案】(1)![]() ;(2)为定值,
;(2)为定值,![]()
【解析】
(1)将![]() 两点坐标代入椭圆方程,建立
两点坐标代入椭圆方程,建立![]() 的方程组,即可求出结论;
的方程组,即可求出结论;
(2)先求出直线![]() 斜率不存在时
斜率不存在时![]() 的值,当直线
的值,当直线![]() 斜率存在时,设其方程为
斜率存在时,设其方程为![]() ,与椭圆方程联立,根据已知求出
,与椭圆方程联立,根据已知求出![]() 关系,再将直线
关系,再将直线![]() 与圆方程联立,根据根与系数关系将
与圆方程联立,根据根与系数关系将![]() 坐标用
坐标用![]() 表示,进而求出
表示,进而求出![]() ,即可得出结论.
,即可得出结论.
(1)依题意, ,解得
,解得 ,
,
所以椭圆方程为![]() .
.
(2)当直线l的斜率不存在时,直线l的方程为![]() .
.
若直线l的方程为![]() ,则M,N的坐标为
,则M,N的坐标为![]() ,
,
![]() .
.
若直线l的方程为![]() ,则M,N的坐标为
,则M,N的坐标为![]() ,
,
![]() .
.
当直线l的斜率存在时,可设直线![]() ,
,
与椭圆方程联立可得![]() ,
,
由相切可得![]() ,
,
![]() .
.
又![]() ,消去
,消去![]() 得
得![]()
![]() ,
,
设![]() ,
,![]() ,则
,则
∴![]() ,
,
![]() .
.
故![]() 为定值且定值为
为定值且定值为![]() .
.
综上,![]() 为定值且定值为
为定值且定值为![]() .
.

【题目】一种室内种植的珍贵草药的株高![]() (单位:
(单位:![]() )与一定范围内的温度
)与一定范围内的温度![]() (单位:
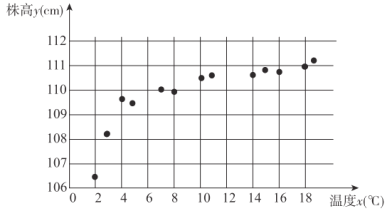
(单位:![]() )有关,现收集了该种草药的13组观测数据,得到如下的散点图,现根据散点图利用
)有关,现收集了该种草药的13组观测数据,得到如下的散点图,现根据散点图利用![]() 或
或![]() 建立
建立![]() 关于
关于![]() 的回归方程,令
的回归方程,令![]() ,
,![]() ,得到如下数据,且
,得到如下数据,且![]() 与
与![]() (
(![]() )的相关系数分别为
)的相关系数分别为![]() ,且
,且![]() .
.
|
|
|
|
10.15 | 109.94 | 3.04 | 0.16 |
|
|
|
|
|
|
|
|
|
|
(1)用相关系数说明哪种模型建立![]() 与
与![]() 的回归方程更合适;
的回归方程更合适;
(2)根据(1)的结果及表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)已知这种草药的利润![]() 与
与![]() ,
,![]() 的关系为
的关系为![]() ,当
,当![]() 为何值时,利润
为何值时,利润![]() 的预报值最大.
的预报值最大.
附:参考公式和数据:对于一组数据![]() (
(![]() ),其回归直线
),其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为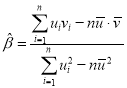 ,
,![]() ,相关系数
,相关系数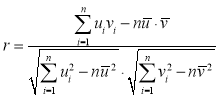 ,
,![]()
【题目】足球是当今世界传播范围最广、参与人数最多的体育运动,具有广泛的社会影响,深受世界各国民众喜爱.
(1)为调查大学生喜欢足球是否与性别有关,随机选取50名大学生进行问卷调查,当问卷评分不低于80分则认为喜欢足球,当评分低于80分则认为不喜欢足球,这50名大学生问卷评分的结果用茎叶图表示如图:
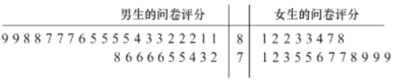
请依据上述数据填写如下列联表:
喜欢足球 | 不喜欢足球 | 总计 | |
女生 |
|
|
|
男生 |
|
|
|
总计 |
|
|
|
请问是否有 ![]() 的把握认为喜欢足球与性别有关?
的把握认为喜欢足球与性别有关?
参考公式及数据: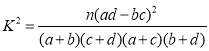 ,
,![]() .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
(2)已知某国“糖果盒”足球场每年平均上座率![]() 与该国成年男子国家足球队在国际足联的年度排名
与该国成年男子国家足球队在国际足联的年度排名![]() 线性相关,数据如表
线性相关,数据如表![]() ,
,![]() ,
,![]() ,
,![]()
年度排名 | 9 |
| 6 |
| 3 |
平均上座率 | 0.9 | 0.91 | 0.92 | 0.93 | 0.95 |
求变量![]() 与
与![]() 的线性回归方程
的线性回归方程![]() ,并预测排名为1时该球场的上座率.
,并预测排名为1时该球场的上座率.
参考公式及数据: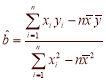 ,
,![]() ;
;![]() .
.
【题目】大学先修课程是在高中开设的具有大学水平的课程,旨在让学有余力的高中生早接受大学思维方式、学习方法的训练,为大学学习乃至未来的职业生涯做好准备.某高中成功开设大学先修课程已有两年,共有![]() 人参与学习先修课程,这两年学习先修课程的学生都参加了高校的自主招生考试(满分
人参与学习先修课程,这两年学习先修课程的学生都参加了高校的自主招生考试(满分![]() 分),结果如下表所示:
分),结果如下表所示:
分数 |
|
|
|
|
|
人数 |
|
|
|
|
|
参加自主招生获得通过的概率 |
|
|
|
|
|
(1)这两年学校共培养出优等生![]() 人,根据图中等高条形图,填写相应列联表,并根据列联表检验能否在犯错的概率不超过
人,根据图中等高条形图,填写相应列联表,并根据列联表检验能否在犯错的概率不超过![]() 的前提下认为学习先修课程与优等生有关系?
的前提下认为学习先修课程与优等生有关系?
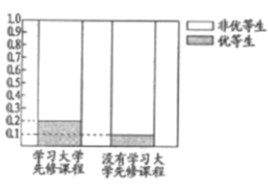
优等生 | 非优等生 | 总计 | |
学习大学先修课程 |
| ||
没有学习大学先修课程 | |||
总计 |
|
(2)已知今年全校有![]() 名学生报名学习大学选项课程,并都参加了高校的自主招生考试,以前两年参加大学先修课程学习成绩的频率作为今年参加大学先修课程学习成绩的概率.
名学生报名学习大学选项课程,并都参加了高校的自主招生考试,以前两年参加大学先修课程学习成绩的频率作为今年参加大学先修课程学习成绩的概率.
(i)在今年参与大学先修课程学习的学生中任取一人,求他获得高校自主招生通过的概率;
(ii)某班有![]() 名学生参加了大学先修课程的学习,设获得高校自主招生通过的人数为
名学生参加了大学先修课程的学习,设获得高校自主招生通过的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式: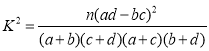 ,其中
,其中![]() .
.