题目内容
已知{an}为等差数列,且a3=-6,a6=0.(Ⅰ)求{an}的通项公式;
(Ⅱ)设bn=|an|,设数列{bn}的前n项和为Sn,求S6和S30.
【答案】分析:(1)设出等差数列的首项和公差后,由a3=-6,a6=0列方程组求解,然后直接代入等差数列通项公式;
(2)由通项大于等于0可解得数列的前6项大于等于0,从第7项开始小于0,则数列{bn}的前6项的和是{an}前6项和的相反数,
前30项的和为{an}的前30项的和减去2倍的前6项的和.
解答:解:(1)设{an}的首项为a1,公差为d,则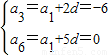 ,解得a1=-10,d=2,所以an=a1+(n-1)d=-10+2(n-1)=2n-12;
,解得a1=-10,d=2,所以an=a1+(n-1)d=-10+2(n-1)=2n-12;
(2)由an=2n-12≥0,得n≥6,所以数列{an}的前5项为负值,a6=0,从第7项开始数列的各项为正值,
则S6=-(a1+a2+…+a6)=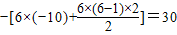 .
.
S30=(a1+a2+…+a30)-2(a1+a2+…+a6)=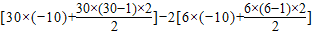 =630.
=630.
点评:本题考查了等差数列的通项公式,考查了等差数列的前n项和,解答此题的关键是明确数列{an}从第几项开始为负值,此题是中档题.
(2)由通项大于等于0可解得数列的前6项大于等于0,从第7项开始小于0,则数列{bn}的前6项的和是{an}前6项和的相反数,
前30项的和为{an}的前30项的和减去2倍的前6项的和.
解答:解:(1)设{an}的首项为a1,公差为d,则
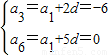 ,解得a1=-10,d=2,所以an=a1+(n-1)d=-10+2(n-1)=2n-12;
,解得a1=-10,d=2,所以an=a1+(n-1)d=-10+2(n-1)=2n-12;(2)由an=2n-12≥0,得n≥6,所以数列{an}的前5项为负值,a6=0,从第7项开始数列的各项为正值,
则S6=-(a1+a2+…+a6)=
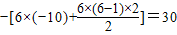 .
.S30=(a1+a2+…+a30)-2(a1+a2+…+a6)=
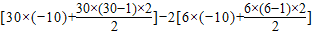 =630.
=630.点评:本题考查了等差数列的通项公式,考查了等差数列的前n项和,解答此题的关键是明确数列{an}从第几项开始为负值,此题是中档题.

练习册系列答案
相关题目