题目内容
(必修5做)已知数列{an},Sn为{an}的前n项和,且有Sn=2an-1,则an=
- A.2n-1
- B.2n
- C.2n-1
- D.2n
C
分析:根据Sn与an的关系式可利用Sn-Sn-1=an(n≥2)消去Sn,从而得到an与an-1的关系,从而可求出数列{an}的通项公式.
解答:当n=1时,a1=S1=2a1-1,∴a1=1.
∵Sn=2an-1,
∴当n≥2时,Sn-1=2an-1-1,
∴Sn-Sn-1=2an-2an-1,
∴an=2an-2an-1,
∴an=2an-1,
∴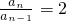 ,
,
∴{an}是首项为1,公比为2的等比数列,
∴an=2n-1,n∈N*.
故选C.
点评:本题主要考查数列的性质和应用,解题时要认真审题,同时考查了 计算能力,属于基础题.
分析:根据Sn与an的关系式可利用Sn-Sn-1=an(n≥2)消去Sn,从而得到an与an-1的关系,从而可求出数列{an}的通项公式.
解答:当n=1时,a1=S1=2a1-1,∴a1=1.
∵Sn=2an-1,
∴当n≥2时,Sn-1=2an-1-1,
∴Sn-Sn-1=2an-2an-1,
∴an=2an-2an-1,
∴an=2an-1,
∴
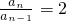 ,
,∴{an}是首项为1,公比为2的等比数列,
∴an=2n-1,n∈N*.
故选C.
点评:本题主要考查数列的性质和应用,解题时要认真审题,同时考查了 计算能力,属于基础题.

练习册系列答案
相关题目
 (必修3做) 在2008年奥运会上甲、乙两名射击运动员在比赛中打出如下成绩:
(必修3做) 在2008年奥运会上甲、乙两名射击运动员在比赛中打出如下成绩: