题目内容
设a、b、c都是正实数，且a、b满足
+
=1，则使a+b≥c恒成立的c的取值范围是（ ）A．（0，8]
B．（0，10]
C．（0，12]
D．（0，16]
【答案】分析：由题意可得a+b=（a+b）（
）=1+
+
+9，再利用基本不等式求出a+b的最小值为16，从而得到16≥c，由此求得c的取值范围．
解答：解：a、b、c都是正实数，且a、b满足
+
=1，则a+b=（a+b）（
）=1+
+
+9=10+
+
≥10+2
=16，
当且仅当
=
时，等号成立．
故a+b的最小值为16，要使a+b≥c恒成立恒成立，只要16≥c，故c的取值范围为（0，16]，
故选D．
点评：本题主要考查基本不等式的应用，注意基本不等式的使用条件，并注意检验等号成立的条件，以及函数的恒成立问题，属于基础题．
）=1+++9，再利用基本不等式求出a+b的最小值为16，从而得到16≥c，由此求得c的取值范围．解答：解：a、b、c都是正实数，且a、b满足
+=1，则a+b=（a+b）（）=1+++9=10++≥10+2=16，当且仅当
=时，等号成立．故a+b的最小值为16，要使a+b≥c恒成立恒成立，只要16≥c，故c的取值范围为（0，16]，
故选D．
点评：本题主要考查基本不等式的应用，注意基本不等式的使用条件，并注意检验等号成立的条件，以及函数的恒成立问题，属于基础题．
练习册系列答案
相关题目
+
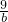=1，则使a+b≥c恒成立的c的取值范围是
≤3
.
+
=1，则使a+b≥c恒成立的c的取值范围是