题目内容
某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在[29.94,30.06)的零件为优质品.从两个分厂生产的零件中各抽出了500件,量其内径尺寸,得结果如下表:
甲厂:
| 分组 | [29.86,29.90) | [29.90,29.94) | [29.94,29.98) | [29.9830.02), | [30.02,30.06) | [30.06,30.10) | [30.10,30.14) |
| 频数 | 12 | 63 | 86 | 182 | 92 | 61 | 4 |
| 分组 | [29.86,29.90) | [29.90,29.94) | [29.94,29.98) | [29.9830.02), | [30.02,30.06) | [30.06,30.10) | [30.10,30.14) |
| 频数 | 29 | 71 | 85 | 159 | 76 | 62 | 18 |
(1)试分别估计两个分厂生产的零件的优质品率;
(2)由以上统计数据填下面2×2列联表,并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”?
| | 甲厂 | 乙厂 | 合计 |
| 优质品 | | | |
| 非优质品 | | | |
| 合 计 | | | |
| P(χ2≥x0) | 0.05 | 0.01 |
| x0 | 3.841 | 6.635 |
(1) 72% 64% (2) 有99%的把握认为“两个分厂生产的零件的质量有差异”
解析解:(1)甲厂抽查的产品中有360件优质品,从而甲厂生产的零件的优质品率估计为 =72%;
=72%;
乙厂抽查的产品中有320件优质品,从而乙厂生产的零件的优质品率估计为 =64%.
=64%.
(2)
χ2= 甲厂 乙厂 合计 优质品 360 320 680 非优质品 140 180 320 合计 500 500 1 000  ≈7.35>6.635,
≈7.35>6.635,
所以有99%的把握认为“两个分厂生产的零件的质量有差异”.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
某工厂有工人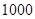 人,其中
人,其中 名工人参加过短期培训(称为
名工人参加过短期培训(称为 类工人),另外
类工人),另外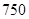 名工人参加过长期培训(称为
名工人参加过长期培训(称为 类工人).现用分层抽样的方法(按
类工人).现用分层抽样的方法(按 类、
类、 类分二层)从该工厂的工人中共抽查
类分二层)从该工厂的工人中共抽查 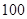 名工人,调查他们的生产能力(此处的生产能力指一天加工的零件数).
名工人,调查他们的生产能力(此处的生产能力指一天加工的零件数).
(1) 类工人和
类工人和 类工人中各抽查多少工人?
类工人中各抽查多少工人?
(2)从 类工人中的抽查结果和从
类工人中的抽查结果和从 类工人中的抽查结果分别如下表1和表2.
类工人中的抽查结果分别如下表1和表2.
表1
| 生产能力分组 | 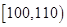 | 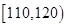 |  | 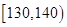 | 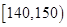 |
| 人数 | 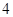 |  |  | 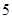 |  |
| 生产能力分组 | 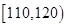 |  | 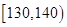 | 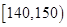 |
| 人数 |  |  |  |  |
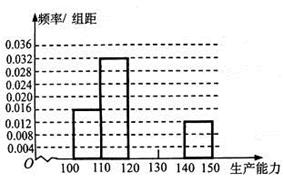
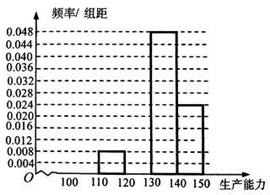
①求
 、
、 ,再完成下列频率分布直方图;
,再完成下列频率分布直方图;②分别估计
 类工人和
类工人和 类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数(同一组
类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数(同一组中的数据用该组区间的中点值作代表).
在某种产品表面进行腐蚀性刻线实验,得到腐蚀深度y与腐蚀时间x之间相应的一组观察值,如下表:
| x/s | 5 | 10 | 15 | 20 | 30 | 40 | 50 | 60 | 70 | 90 | 120 |
| y/μm | 6 | 10 | 10 | 13 | 16 | 17 | 19 | 23 | 25 | 29 | 46 |
随着工业化以及城市车辆的增加,城市的空气污染越来越严重,空气质量指数API一直居高不下,对人体的呼吸系统造成了严重的影响.现调查了某市500名居民的工作场所和呼吸系统健康,得到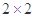 列联表如下:
列联表如下:
| | 室外工作 | 室内工作 | 合计 |
| 有呼吸系统疾病 | 150 | | |
| 无呼吸系统疾病 | | 100 | |
| 合计 | 200 | | |
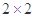 列联表;
列联表;(2)你是否有95%的把握认为感染呼吸系统疾病与工作场所有关;
(3)现采用分层抽样从室内工作的居民中抽取一个容量为6的样本,将该样本看成一个总体,从中随机的抽取两人,求两人都有呼吸系统疾病的概率.
参考公式与临界值表:K2=
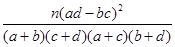
| P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
从发生汽车碰撞事故的司机中抽取2 000名司机.根据他们的血液中是否含有酒精以及他们是否对事故负有责任.将数据整理如下:
| | 有责任 | 无责任 | 合计 |
| 有酒精 | 650 | 150 | 800 |
| 无酒精 | 700 | 500 | 1 200 |
| 合计 | 1 350 | 650 | 2 000 |
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据.
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程
 =bx+a.
=bx+a.(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)



 表示抽到“极幸福”的人数,求
表示抽到“极幸福”的人数,求