题目内容

将函数y=sin(2x+
π
4
)的图象向左平移
π
4
个单位，再向上平移2个单位，则所得图象的一个对称中心是（　　）
分析：根据函数图象平移公式，所得图象对应函数为y=sin(2x+
3π
4
)+2，再由三角函数图象对称中心的公式解关于x的方程，即可得到所得图象的一个对称中心．
解答：解：∵f（x）=sin(2x+
π
4
)，
∴图象向左平移
π
4
个单位，再向上平移2个单位，得y=f（x+
π
4
）+2=sin(2x+
3π
4
)+2的图象
令2x+
3π
4
=kπ，k∈Z，得x=-
3π
8
+
1
2
kπ，k∈Z，
取k=1，得x=-
3π
8
+
π
2
=
π
8

∴所得图象的一个对称中心是（
π
8
，2）
故选：C
点评：本题给出三角函数图象的平移，求所得图象的一个对称中心，着重考查了三角函数的图象与变换、函数图象对称中心公式等知识，属于基础题．
练习册系列答案
相关题目
给出下列命题：
①在△ABC中，若A＜B，则sinA＜sinB；
②将函数y=sin(2图象向右平移
π
3
个单位，得到函数y=sin2x的图象；
③在△ABC中，若AB=2，AC=3，∠ABC=60°，则△ABC必为锐角三角形；
④在同一坐标系中，函数y=sinx的图象和函数y=
x
2
的图象有三个公共点．
其中真命题是
 
．（填出所有正确命题的序号）
将函数y=sin(6x+
π
4
)的图象上各点的横坐标伸长到原来的3倍，再向右平移
π
8
个单位，得到的函数的一个对称中心（　　）
将函数y=sin(x+
π
3
)的图象向右平移
π
6
个单位，再向上平移2个单位所得图象对应的函数解析式是
y=sin(x+
π
6
)+2
y=sin(x+
π
6
)+2
．
将函数y=sin(
1
2
x+
π
3
)的图象作如下那种变换，才能得到函数y=sin(
1
2
x)的图象（　　）

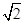要得到函数y=cos(2+)的图象, 只需要将函数y=sin(2+)图象上所有的点(     )

A．向左平移个单位，纵坐标不变；

B．向右平移个单位，纵坐标不变；

C．向左平移个单位，纵坐标不变；

D．向右平移 个单位，纵坐标不变．

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网