题目内容
设f(x)= 是奇函数(a>0且a≠1),
是奇函数(a>0且a≠1),
(1)求出m的值
(2)若f(x)的定义域为[α,β](β>α>1),
判断f(x)在定义域上的增减性,并加以证明.
解:(1)由题意可得f(-x)+f(x)=0 …
即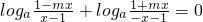
∴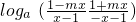 =
=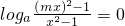
∴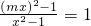 …
…
∴(mx)2-1=x2-1
∴m=±1
∴m=-1 m=1(舍) …
(2)当0<m<1时,f(x)为增函数;m>1时,f(x)为减函数,判断如下
∵f(x)的定义域为[α,β](β>α>0),则[α,β]?(1,+∞).
设x1,x2∈[α,β],则1<x1<x2
f(x1)-f(x2)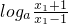
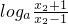 =loga
=loga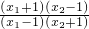
∵(1+x1)(x2-1)-(x1-1)(1+x2)=2(x2-x1)>0
∴(1+x1)(x2-1)>(x1-1)(1+x2)即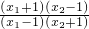 >1
>1
∴当0<m<1时,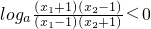 ,即f(x1)<f(x2);
,即f(x1)<f(x2);
当m>1时,loga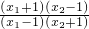 >0,即定义在证明函数f(x1)>f(x2),
>0,即定义在证明函数f(x1)>f(x2),
故当0<m<1时,f(x)为增函数;m>1时,f(x)为减函数. …
分析:(1)由 题意可得f(-x)=-f(x),代入可求m
(2)利用函数单调性的定义即可证明:设x1,x2∈[α,β],则1<x1<x2,对函数值作差f(x1)-f(x2)=loga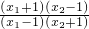 结合已知可判断
结合已知可判断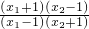 的正负,进而讨论当0<m<1时,及m>1时,f(x1)-f(x2)的符号,即可证明
的正负,进而讨论当0<m<1时,及m>1时,f(x1)-f(x2)的符号,即可证明
点评:本题主要考查了奇函数的定义f(-x)=-f(x)的应用,及函数的单调性及函数的单调性的定义在证明函数单调中的应用,属于函数知识的综合应用
即
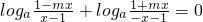
∴
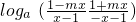 =
=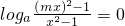
∴
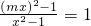 …
…∴(mx)2-1=x2-1
∴m=±1
∴m=-1 m=1(舍) …
(2)当0<m<1时,f(x)为增函数;m>1时,f(x)为减函数,判断如下
∵f(x)的定义域为[α,β](β>α>0),则[α,β]?(1,+∞).
设x1,x2∈[α,β],则1<x1<x2
f(x1)-f(x2)
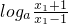
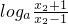 =loga
=loga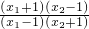
∵(1+x1)(x2-1)-(x1-1)(1+x2)=2(x2-x1)>0
∴(1+x1)(x2-1)>(x1-1)(1+x2)即
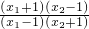 >1
>1∴当0<m<1时,
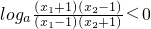 ,即f(x1)<f(x2);
,即f(x1)<f(x2);当m>1时,loga
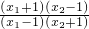 >0,即定义在证明函数f(x1)>f(x2),
>0,即定义在证明函数f(x1)>f(x2),故当0<m<1时,f(x)为增函数;m>1时,f(x)为减函数. …
分析:(1)由 题意可得f(-x)=-f(x),代入可求m
(2)利用函数单调性的定义即可证明:设x1,x2∈[α,β],则1<x1<x2,对函数值作差f(x1)-f(x2)=loga
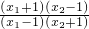 结合已知可判断
结合已知可判断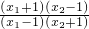 的正负,进而讨论当0<m<1时,及m>1时,f(x1)-f(x2)的符号,即可证明
的正负,进而讨论当0<m<1时,及m>1时,f(x1)-f(x2)的符号,即可证明点评:本题主要考查了奇函数的定义f(-x)=-f(x)的应用,及函数的单调性及函数的单调性的定义在证明函数单调中的应用,属于函数知识的综合应用

练习册系列答案
相关题目
下列命题中正确的是( )
A、设f(x)=sin(2x+
| ||||||
B、?x0∈R.便得
| ||||||
C、设f(x)=cos(x+
| ||||||
D、设f(x)=2sin2x,则f(x+
|