题目内容
在△ABC中,a、b、c分别为角A、B、C的对边,设f(x)=a2x2-(a2-b2)x-4c2.(1)若
 ,求角C的大小;
,求角C的大小;(2)若f(2)=0,求角C的取值范围.
【答案】分析:(1)由题意可得:a2-(a2-b2)-4c2=0,即可得到b=2c,根据正弦定理可得:sinB=2sinC,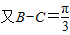 ,可得
,可得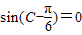 ,再结合角C的范围求出答案即可.
,再结合角C的范围求出答案即可.
(2)由题意可得:a2+b2=2c2,根据余弦定理可得: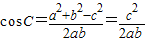 再由2c2=a2+b2≥2ab可得ab≤c2,进而求出cosC的范围即可根据余弦函数求出角C的范围.
再由2c2=a2+b2≥2ab可得ab≤c2,进而求出cosC的范围即可根据余弦函数求出角C的范围.
解答:解:(1)由题意可得:f(1)=0,
∴a2-(a2-b2)-4c2=0,
∴b2=4c2,即b=2c,
∴根据正弦定理可得:sinB=2sinC.
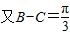 ,可得
,可得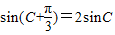 ,
,
∴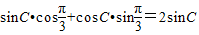 ,
,
∴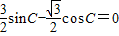 ,
,
∴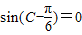 .
.
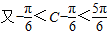 ,
,
∴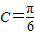 .
.
(2)若f(2)=0,则4a2-2(a2-b2)-4c2=0,
∴a2+b2=2c2,
∴根据余弦定理可得: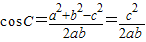 .
.
又2c2=a2+b2≥2ab,
∴ab≤c2.
∴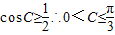 .
.
点评:本题主要考查两角和与差的正弦函数,以及正弦定理与余弦定理等知识点,解决此类问题的关键是熟练掌握有关的公式与定理,并且进行正确的运算.
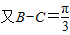 ,可得
,可得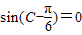 ,再结合角C的范围求出答案即可.
,再结合角C的范围求出答案即可.(2)由题意可得:a2+b2=2c2,根据余弦定理可得:
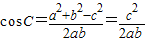 再由2c2=a2+b2≥2ab可得ab≤c2,进而求出cosC的范围即可根据余弦函数求出角C的范围.
再由2c2=a2+b2≥2ab可得ab≤c2,进而求出cosC的范围即可根据余弦函数求出角C的范围.解答:解:(1)由题意可得:f(1)=0,
∴a2-(a2-b2)-4c2=0,
∴b2=4c2,即b=2c,
∴根据正弦定理可得:sinB=2sinC.
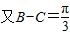 ,可得
,可得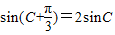 ,
,∴
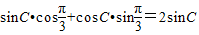 ,
,∴
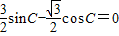 ,
,∴
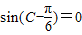 .
.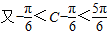 ,
,∴
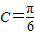 .
.(2)若f(2)=0,则4a2-2(a2-b2)-4c2=0,
∴a2+b2=2c2,
∴根据余弦定理可得:
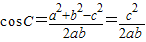 .
.又2c2=a2+b2≥2ab,
∴ab≤c2.
∴
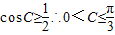 .
.点评:本题主要考查两角和与差的正弦函数,以及正弦定理与余弦定理等知识点,解决此类问题的关键是熟练掌握有关的公式与定理,并且进行正确的运算.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在△ABC中,∠A、∠B、∠C所对的边长分别是a、b、c.满足2acosC+ccosA=b.则sinA+sinB的最大值是( )
A、
| ||||
| B、1 | ||||
C、
| ||||
D、
|