Question

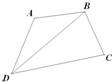如图，四边形ABCD中，AB=

2

，BC=2，CD=3，∠A=120°，∠ADB=45°，则cosC的值为（　　）

• A．

  5

  6

• B．

  3

  4

• C．

  2

  3

• D．

  1

  2

Answer 1

分析：△ABD中，由正弦定理求得BD的值，在△BCD中，由余弦定理求得 cosC 的值．

解答：解：由题意得 AB=

2

，BC=2，CD=3，∠A=120°，∠ADB=45°，
在△ABD中，由正弦定理可得

BD

sinA

=

AB

sin∠ADB

，即

BD

3 2

=

2

2 2

，解得BD=

3

．
在△BCD中，由余弦定理可得 cosC=

CB2+CD2-BD2

2CB•CD

=

4+9-3

2×2×3

=

5

6

，
故选A．

点评：本题主要考查正弦定理和余弦定理的应用，属于中档题．