题目内容
 ________.
________.
5005
分析:化简项公式为 Tr+1=(-1)rCr15 ,令30-5r=0,可得r=6,可得常数项为 C156=5005.
,令30-5r=0,可得r=6,可得常数项为 C156=5005.
解答:二项展开式的通项公式为 Tr+1=C15r (-1)r
(-1)r 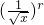 =(-1)rCr15
=(-1)rCr15  .
.
令30-5r=0,可得r=6.
故常数项为 C156=5005,
故答案为:5005.
点评:本题考查二项式定理,二项展开式的通项公式,求展开式中某项的系数,化简项公式为 Tr+1=(-1)rCr15 ,
,
是解题的关键.
分析:化简项公式为 Tr+1=(-1)rCr15
 ,令30-5r=0,可得r=6,可得常数项为 C156=5005.
,令30-5r=0,可得r=6,可得常数项为 C156=5005.解答:二项展开式的通项公式为 Tr+1=C15r
 (-1)r
(-1)r 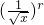 =(-1)rCr15
=(-1)rCr15  .
.令30-5r=0,可得r=6.
故常数项为 C156=5005,
故答案为:5005.
点评:本题考查二项式定理,二项展开式的通项公式,求展开式中某项的系数,化简项公式为 Tr+1=(-1)rCr15
 ,
,是解题的关键.

练习册系列答案
相关题目
某校从高二年级4个班中选出18名学生参加全国数学联赛,学生来源人数如表:
| 班别 | 高二(1)班 | 高二(2)班 | 高二(3)班 | 高二(4)班 |
| 人数 | 4 | 6 | 3 | 5 |
(Ⅱ)若要求从18位同学中选出两位同学介绍学习经验,设其中来自高二(1)班的人数为ξ,求随机变量ξ的分布列及数学期望Eξ.
 是关于x的方程x2-kx+k2-3=0的两个实根,且
是关于x的方程x2-kx+k2-3=0的两个实根,且 ,则cosα+sinα=________
,则cosα+sinα=________ .试确定m,n的值或取值范围,使:
.试确定m,n的值或取值范围,使: ,则
,则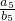 的值为
的值为
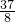





 ,则sin2a=________.
,则sin2a=________.