题目内容
函数 的一个单调减区间为________.
的一个单调减区间为________.
(0,+∞)
分析:分x≥0,x<0两种情况去掉绝对值符号,然后利用导数即可求得单调区间.
解答:(1)当x≥0时,y= -4x+5,
-4x+5,
-2x≤0, >0,ln2>0,
>0,ln2>0,
∴y′= ln
ln •2x-4=-2x
•2x-4=-2x ln2-4<0,
ln2-4<0,
所以函数在(0,+∞)上递减;
(2)当x<0时,-2x>0, >0,ln2>0,
>0,ln2>0,
∴y′= ln
ln •2x+4=-2x
•2x+4=-2x ln2+4>0,
ln2+4>0,
所以函数在(-∞,0)上递增;
故答案为:(0,+∞).
点评:本题考查利用导数研究函数的单调性,考查分类讨论思想,属中档题.
分析:分x≥0,x<0两种情况去掉绝对值符号,然后利用导数即可求得单调区间.
解答:(1)当x≥0时,y=
 -4x+5,
-4x+5,-2x≤0,
 >0,ln2>0,
>0,ln2>0,∴y′=
 ln
ln •2x-4=-2x
•2x-4=-2x ln2-4<0,
ln2-4<0,所以函数在(0,+∞)上递减;
(2)当x<0时,-2x>0,
 >0,ln2>0,
>0,ln2>0,∴y′=
 ln
ln •2x+4=-2x
•2x+4=-2x ln2+4>0,
ln2+4>0,所以函数在(-∞,0)上递增;
故答案为:(0,+∞).
点评:本题考查利用导数研究函数的单调性,考查分类讨论思想,属中档题.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
 的一个单调减区间为
的一个单调减区间为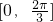
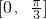
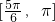

 的一个单调减区间为_______.
的一个单调减区间为_______. 的一个单调减区间为( )
的一个单调减区间为( )


