题目内容
已知数列{an}的前n项和Sn是n的二次函数,且a1=-2,a2=2,a3=6.(1)求Sn的表达式;
(2)求通项an.
解;(1)设Sn=an2+bn+c,(a≠0),
则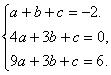 解得
解得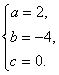
∴Sn=2n2-4n.
(2)∵a1=S1=-2,n≥2时,
∵an=Sn-Sn-1=2n2-4n-2(n-1)2+4(n-1)=4n-6,
∴an=4n-6(n∈N*).

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
已知数列{an}的前n项和Sn=an2+bn(a、b∈R),且S25=100,则a12+a14等于( )
| A、16 | B、8 | C、4 | D、不确定 |