题目内容
.(本小题满分12分)
已知角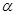 的顶点在原点,始边与
的顶点在原点,始边与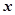 轴的正半轴重合,终边经过点
轴的正半轴重合,终边经过点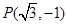 .
.
(Ⅰ)求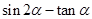 的值;
的值;
(Ⅱ)若函数 ,求函数
,求函数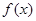 在
在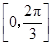 上的单调递增区间.
上的单调递增区间.
已知角
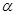 的顶点在原点,始边与
的顶点在原点,始边与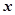 轴的正半轴重合,终边经过点
轴的正半轴重合,终边经过点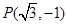 .
. (Ⅰ)求
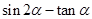 的值;
的值;(Ⅱ)若函数
 ,求函数
,求函数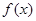 在
在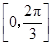 上的单调递增区间.
上的单调递增区间. (Ⅰ) ;
;
(Ⅱ)函数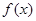 在上的单调递增区间是
在上的单调递增区间是
 ;
;(Ⅱ)函数
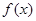 在上的单调递增区间是
在上的单调递增区间是
本试题主要是考查了三角函数的定义以及三角函数的图像与性质的综合运用。
(1)根据角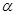 的顶点在原点,始边与
的顶点在原点,始边与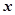 轴的正半轴重合,终边经过点
轴的正半轴重合,终边经过点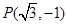 . 得到
. 得到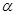 的正弦值和余弦值和正切值,得到
的正弦值和余弦值和正切值,得到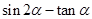 的值;
的值;
(2)因为函数 ,化为单一三角函数,运用二倍角公式展开,可知函数
,化为单一三角函数,运用二倍角公式展开,可知函数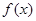 在
在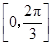 上的单调递增区间
上的单调递增区间
解:(Ⅰ)因为角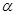 终边经过点
终边经过点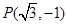 ,
,
 ,
, ,
, ………………3分
………………3分
 ……………6分
……………6分
(Ⅱ) …8分
…8分

当 ,即
,即 时,函数
时,函数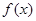 单调递增, …………11分
单调递增, …………11分
所以函数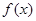 在上的单调递增区间是
在上的单调递增区间是 ………………12分
………………12分
(1)根据角
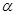 的顶点在原点,始边与
的顶点在原点,始边与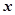 轴的正半轴重合,终边经过点
轴的正半轴重合,终边经过点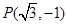 . 得到
. 得到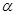 的正弦值和余弦值和正切值,得到
的正弦值和余弦值和正切值,得到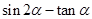 的值;
的值;(2)因为函数
 ,化为单一三角函数,运用二倍角公式展开,可知函数
,化为单一三角函数,运用二倍角公式展开,可知函数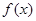 在
在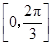 上的单调递增区间
上的单调递增区间解:(Ⅰ)因为角
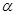 终边经过点
终边经过点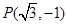 ,
, ,
, ,
, ………………3分
………………3分  ……………6分
……………6分(Ⅱ)
 …8分
…8分
当
 ,即
,即 时,函数
时,函数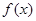 单调递增, …………11分
单调递增, …………11分所以函数
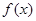 在上的单调递增区间是
在上的单调递增区间是 ………………12分
………………12分
练习册系列答案
相关题目
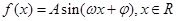 (其中
(其中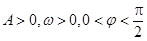 )的图象与x轴的交点中,相邻两个交点之间的距离为
)的图象与x轴的交点中,相邻两个交点之间的距离为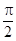 ,且图象上一个最低点为
,且图象上一个最低点为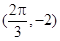 .
.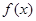 的解析式;
的解析式; 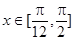 ,求
,求 的图象向左平移
的图象向左平移 个单位,所得图象的函数解析式为 ( )
个单位,所得图象的函数解析式为 ( )
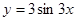


 的性质,并在此基础上,作出其在
的性质,并在此基础上,作出其在
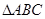 的内角
的内角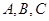 对边的边长分别是
对边的边长分别是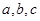 ,
,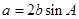 .
.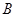 的大小;
的大小;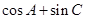 的取值范围.
的取值范围.  的最小正周期( )
的最小正周期( )



 是( )
是( ) 奇函数
奇函数  偶函数
偶函数  非奇非偶函数
非奇非偶函数  不确定
不确定 (ω>0)在区间
(ω>0)在区间 上的最小值是
上的最小值是 ,则ω的最小值为( )
,则ω的最小值为( )


