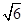题目内容
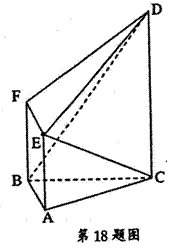
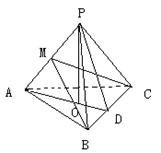
如图,在四面体 中,平面
中,平面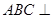 平面
平面 ,
,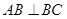 ,
,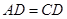 ,
,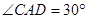 。
。
(Ⅰ)若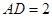 ,
, ,求四面体
,求四面体 的体积;
的体积;
(Ⅱ)若二面角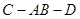 为
为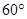 ,求异面直线
,求异面直线 与
与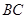 所成角的余弦值。(12分)
所成角的余弦值。(12分)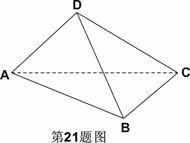
 中,平面
中,平面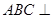 平面
平面 ,
,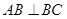 ,
,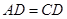 ,
,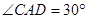 。
。(Ⅰ)若
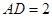 ,
, ,求四面体
,求四面体 的体积;
的体积;(Ⅱ)若二面角
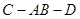 为
为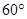 ,求异面直线
,求异面直线 与
与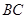 所成角的余弦值。(12分)
所成角的余弦值。(12分)
(1) ;(2)
;(2)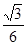 .
.
 ;(2)
;(2)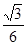 .
.第一问中,利用求解体积知道高和底面积即可。因为设F为AC的中点,由于AD=CD,所以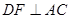 ,故由平面ABC
,故由平面ABC 平面ACD,知
平面ACD,知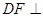 平面ABC,即DF是四面体ABCD的面ABC上的高,再利用由勾股定理易知
平面ABC,即DF是四面体ABCD的面ABC上的高,再利用由勾股定理易知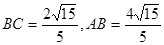 ,得到体积。
,得到体积。
第二问中,设G、H分别为边CD、BD的中点,则FG//AD,GH//BC,
从而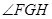 是异面直线AD与BC所成的角或补角设E为边AB的中点,则EF//BC,由
是异面直线AD与BC所成的角或补角设E为边AB的中点,则EF//BC,由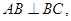 知
知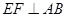 ,又由(1)有
,又由(1)有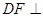 平面ABC,故由三垂线定理知
平面ABC,故由三垂线定理知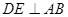 ,
,
所以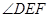 为二面角C—AB—D的平面角,由题设知
为二面角C—AB—D的平面角,由题设知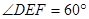 ,设AD=a,则
,设AD=a,则 ,在
,在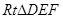 中,
中,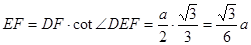
从而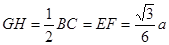 ,因为
,因为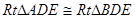 ,故
,故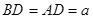 ,
,
从而,在 中,
中, ,又
,又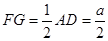 ,从而在
,从而在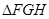 中,因
中,因 再利用余弦定理求解得到异面直线所成的角。
再利用余弦定理求解得到异面直线所成的角。
解:(I)如图,设F为AC的中点,由于AD=CD,所以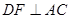 ,
,
故由平面ABC 平面ACD,知
平面ACD,知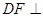 平面ABC,
平面ABC,
即DF是四面体ABCD的面ABC上的高,
且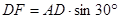 =1,……….2分,
=1,……….2分,

 ,在
,在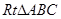 中,
中,
因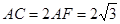 ,
, ,
,
由勾股定理易知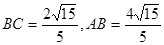 ,
,
故四面体ABCD的体积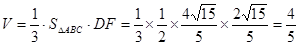 ………….4分
………….4分
(II)如图,设G、H分别为边CD、BD的中点,则FG//AD,GH//BC,
从而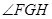 是异面直线AD与BC所成的角或补角。……….6分,
是异面直线AD与BC所成的角或补角。……….6分,
设E为边AB的中点,则EF//BC,由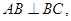 知
知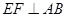 ,
,
又由(1)有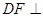 平面ABC,故由三垂线定理知
平面ABC,故由三垂线定理知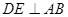 ,
,
所以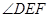 为二面角C—AB—D的平面角,
为二面角C—AB—D的平面角,
由题设知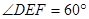 ,……….8分,
,……….8分,
设AD=a,则 ,在
,在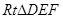 中,
中,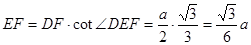 ,
,
从而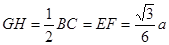 ,因为
,因为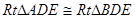 ,故
,故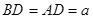 ,从而,在
,从而,在 中,
中, ,又
,又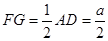 ,从而在
,从而在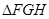 中,因
中,因 ,由余弦定理得
,由余弦定理得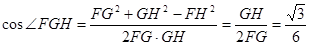 ,
,
因此,异面直线AD与BC所成角的余弦值为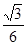 。…….12分
。…….12分
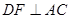 ,故由平面ABC
,故由平面ABC 平面ACD,知
平面ACD,知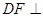 平面ABC,即DF是四面体ABCD的面ABC上的高,再利用由勾股定理易知
平面ABC,即DF是四面体ABCD的面ABC上的高,再利用由勾股定理易知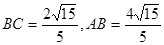 ,得到体积。
,得到体积。第二问中,设G、H分别为边CD、BD的中点,则FG//AD,GH//BC,
从而
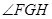 是异面直线AD与BC所成的角或补角设E为边AB的中点,则EF//BC,由
是异面直线AD与BC所成的角或补角设E为边AB的中点,则EF//BC,由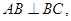 知
知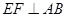 ,又由(1)有
,又由(1)有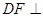 平面ABC,故由三垂线定理知
平面ABC,故由三垂线定理知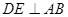 ,
,所以
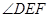 为二面角C—AB—D的平面角,由题设知
为二面角C—AB—D的平面角,由题设知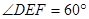 ,设AD=a,则
,设AD=a,则 ,在
,在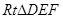 中,
中,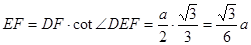
从而
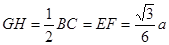 ,因为
,因为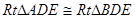 ,故
,故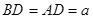 ,
,从而,在
 中,
中, ,又
,又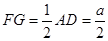 ,从而在
,从而在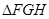 中,因
中,因 再利用余弦定理求解得到异面直线所成的角。
再利用余弦定理求解得到异面直线所成的角。解:(I)如图,设F为AC的中点,由于AD=CD,所以
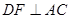 ,
,故由平面ABC
 平面ACD,知
平面ACD,知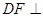 平面ABC,
平面ABC,即DF是四面体ABCD的面ABC上的高,
且
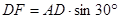 =1,……….2分,
=1,……….2分,
 ,在
,在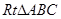 中,
中,因
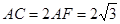 ,
, ,
,由勾股定理易知
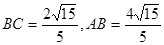 ,
,故四面体ABCD的体积
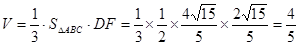 ………….4分
………….4分(II)如图,设G、H分别为边CD、BD的中点,则FG//AD,GH//BC,
从而
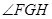 是异面直线AD与BC所成的角或补角。……….6分,
是异面直线AD与BC所成的角或补角。……….6分,设E为边AB的中点,则EF//BC,由
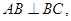 知
知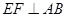 ,
,又由(1)有
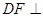 平面ABC,故由三垂线定理知
平面ABC,故由三垂线定理知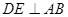 ,
,所以
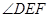 为二面角C—AB—D的平面角,
为二面角C—AB—D的平面角,由题设知
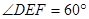 ,……….8分,
,……….8分,设AD=a,则
 ,在
,在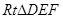 中,
中,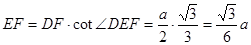 ,
,从而
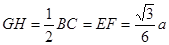 ,因为
,因为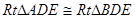 ,故
,故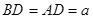 ,从而,在
,从而,在 中,
中, ,又
,又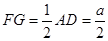 ,从而在
,从而在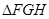 中,因
中,因 ,由余弦定理得
,由余弦定理得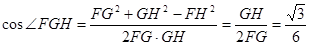 ,
,因此,异面直线AD与BC所成角的余弦值为
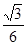 。…….12分
。…….12分

练习册系列答案
相关题目
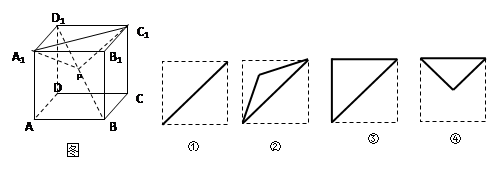
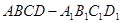 的棱长为
的棱长为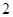 ,
,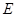 为
为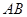 的中点.
的中点.
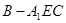 的体积;
的体积;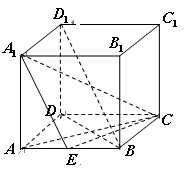
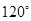 时,过圆锥顶点的截面中,最大截面面积为( )
时,过圆锥顶点的截面中,最大截面面积为( )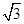
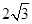
 中,
中, ,
, ,则四棱锥
,则四棱锥 的体积为 ▲ cm3.
的体积为 ▲ cm3.
 的长方形的四个角切去四个相同的正方形,然后折成一个无盖的长方体形的盒子,若这个长方体的外接球的体积存在最小值,则
的长方形的四个角切去四个相同的正方形,然后折成一个无盖的长方体形的盒子,若这个长方体的外接球的体积存在最小值,则 的取值范围是 .
的取值范围是 .