题目内容
设函数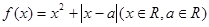 .
.
(I)当 时,求
时,求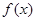 的单调区间;
的单调区间;
(II)若 对
对 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(I)减区间为(- ,
, ),增区间为(
),增区间为( ,+
,+ )(II)
)(II)
解析试题分析:解:(1)当a=2时:f(x)=  +
+ =
=
 原函数的减区间为(-
原函数的减区间为(- ,
, ),增区间为(
),增区间为( ,+
,+ );
);
(2)∵x (-1,3)
(-1,3)  f(x)<10可变为
f(x)<10可变为 -10<a-x< 10-
-10<a-x< 10-
即
对(*):令g(x)=  +x-10,其对称轴为
+x-10,其对称轴为
 ③
③
对②令
 ④
④
由③、④知:
考点:函数的单调区间;绝对值不等式
点评:求含有绝对值的函数,常将函数变为分段函数。对于求不等式中常数的范围,常要分步讨论。

练习册系列答案
 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
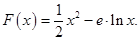
 的最小值;
的最小值;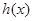 和
和 定义域内的任意实数
定义域内的任意实数 ,若存在常数
,若存在常数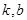 ,使得不等式
,使得不等式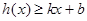 和
和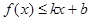 都成立,则称直线
都成立,则称直线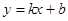 是函数
是函数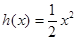 ,
,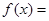
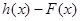 ,试问函数
,试问函数 的空气隔层.根据热传导知识,对于厚度为
的空气隔层.根据热传导知识,对于厚度为 的均匀介质,两侧的温度差为
的均匀介质,两侧的温度差为 ,单位时间内,在单位面积上通过的热量
,单位时间内,在单位面积上通过的热量 ,其中
,其中 为热传导系数.假定单位时间内,在单位面积上通过每一层玻璃及空气隔层的热量相等.(注:玻璃的热传导系数为
为热传导系数.假定单位时间内,在单位面积上通过每一层玻璃及空气隔层的热量相等.(注:玻璃的热传导系数为 ,空气的热传导系数为
,空气的热传导系数为 .)
.)
 ,
, ,内层玻璃外侧温度为
,内层玻璃外侧温度为 ,外层玻璃内侧温度为
,外层玻璃内侧温度为 ,且
,且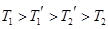 .试分别求出单层玻璃和双层中空玻璃单位时间内,在单位面积上通过的热量(结果用
.试分别求出单层玻璃和双层中空玻璃单位时间内,在单位面积上通过的热量(结果用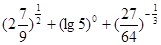 ;(2)解方程:log3(6x-9)=3.
;(2)解方程:log3(6x-9)=3. 
 .
.  时取得极值?说明理由;
时取得极值?说明理由; ,4]时,函数f(x)与g(x)的图像有两个公共点,求c的取值范围.
,4]时,函数f(x)与g(x)的图像有两个公共点,求c的取值范围. 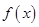 是定义在(0,+∞)上的增函数,且满足
是定义在(0,+∞)上的增函数,且满足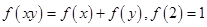 .
.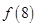 的值; (2)求不等式
的值; (2)求不等式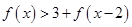 的解集.
的解集. (0
(0 x
x 平方米,矩形一边的长为
平方米,矩形一边的长为 米(如图所示)
米(如图所示)
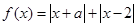
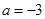 时,求不等式
时,求不等式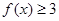 的解集; (2)若
的解集; (2)若 的解集包含
的解集包含 ,求
,求 的取值范围.
的取值范围.